
Two identical charged spheres are suspended by strings of equal lengths. The strings make an angle of
A). 4
B). 3
C). 2
D). 1
Answer
504.3k+ views
Hint In order to solve this question first we have to draw a proper diagram and then we will proceed further by equating the forces applied on the ball with the help of the diagram. We will use the concept of trigonometry along with the concept of electrostatics.
Formula used:
Complete step-by-step solution:
Figure:
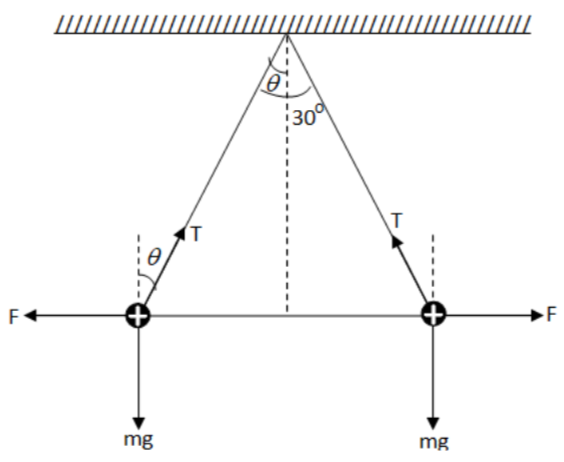
Initially, the forces acting on each ball are
(i) Tension T
(ii) Weight mg (m=mass of the ball in kg , g = acceleration due to gravity in
(iii) The electrostatic force of repulsion F for its equilibrium along vertical, where
And along horizontal, we have
Dividing equation (2) by (1), we get
Now ,when the balls are suspended in a liquid of density σ and dielectric constant
while weight becomes original weight - Upthrust.
But before that let us know about Upthrust, which can be defined as the upward force applied by a liquid on an object immersed (partially or fully) or floating in the liquid. Mathematically it can be written as
Taking mg as common , we get
Now ,for the equilibrium of the balls we need a relation between the new or apparent force and the apparent weight, given as below
Angle changes from
Now , Let us substitute the value of mg’ from equation (4) in equation (5)
So we get:
Let us find the value of
And we know
As we know from the given problem statement:
Now, from equation (6) and equation (3), we have
Let us now solve this equation to find the value of the dielectric constant K.
As we have been given in the problem, the density is
Hence, the dielectric constant of the liquid is 2
So, the correct answer is option C.
Note: The relative permittivity of a substance, or dielectric constant, is its permittivity expressed as a ratio to the permittivity of the vacuum. Permittivity is a material property that has an effect on the Coulomb force in the material between two point charges. Two or more solid objects in touch are exerting forces on one another. We give different names to those contact forces based on the objects in contact. When a loop, cord, wire, or spring happens to be one of those objects in contact, we call friction as stress.
Formula used:
Complete step-by-step solution:
Figure:

Initially, the forces acting on each ball are
(i) Tension T
(ii) Weight mg (m=mass of the ball in kg , g = acceleration due to gravity in
(iii) The electrostatic force of repulsion F for its equilibrium along vertical, where
And along horizontal, we have
Dividing equation (2) by (1), we get
Now ,when the balls are suspended in a liquid of density σ and dielectric constant
while weight becomes original weight - Upthrust.
But before that let us know about Upthrust, which can be defined as the upward force applied by a liquid on an object immersed (partially or fully) or floating in the liquid. Mathematically it can be written as
Taking mg as common , we get
Now ,for the equilibrium of the balls we need a relation between the new or apparent force and the apparent weight, given as below
Angle changes from
Now , Let us substitute the value of mg’ from equation (4) in equation (5)
So we get:
Let us find the value of
And we know
As we know from the given problem statement:
Now, from equation (6) and equation (3), we have
Let us now solve this equation to find the value of the dielectric constant K.
As we have been given in the problem, the density is
Hence, the dielectric constant of the liquid is 2
So, the correct answer is option C.
Note: The relative permittivity of a substance, or dielectric constant, is its permittivity expressed as a ratio to the permittivity of the vacuum. Permittivity is a material property that has an effect on the Coulomb force in the material between two point charges. Two or more solid objects in touch are exerting forces on one another. We give different names to those contact forces based on the objects in contact. When a loop, cord, wire, or spring happens to be one of those objects in contact, we call friction as stress.
Recently Updated Pages
Basicity of sulphurous acid and sulphuric acid are

Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Biology: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Master Class 4 Maths: Engaging Questions & Answers for Success

Trending doubts
Give 10 examples of unisexual and bisexual flowers

Draw a labelled sketch of the human eye class 12 physics CBSE

a Tabulate the differences in the characteristics of class 12 chemistry CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Why is the cell called the structural and functional class 12 biology CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE




