Question

Two identical coils are placed coaxially with their centres separated by a distance of 0.1m. A current of 0.5A passes through each coil in opposite directions. If the radius of either coil is 0.5m and the number of turns in each coil is 40. Find the resultant magnetic field at the centre of either coils.

Answer 1

Hint: First find the magnetic field at the centre of one coil due its current and the current in the other coil by using the formula for the magnitude of magnetic field due to a coil at a point on in its axis, at a distance of x from its centre. Find the direction of the field with the right hand rule.

Formula used:
$B=\dfrac{N{{\mu }_{0}}i{{R}^{2}}}{2{{\left( {{R}^{2}}+{{x}^{2}} \right)}^{\dfrac{3}{2}}}}$

Complete step-by-step answer:
Let us first draw a diagram with the given information. It is said that there are two coils (in the shape of a circular ring) placed coaxially. Meaning, the standard axes of both the coils coincide. It is also said that the distance between the centres of the two coils is 0.1m
The currents in both the coils are the same but are opposite in directions. The current is given to be 0.5A.
Let us find the resultant magnetic field at the centre (O) of coil 1 due to the current in it and the current in coil 2.
The magnetic field at point O due the coil 1 be ${{B}_{1}}$ and the magnetic field due to coil 2 be ${{B}_{2}}$.
The direction of the magnetic field is given by the right hand rule.

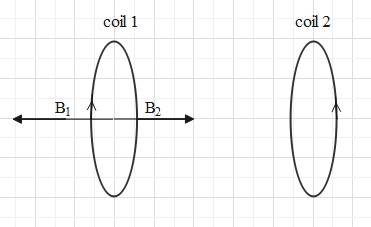
According to the rule, the direction of ${{B}_{1}}$ will be towards left and the direction of ${{B}_{2}}$ will be towards right.
The direction of the magnetic field is given by the right hand rule.
According to the rule, the direction of ${{B}_{1}}$ will be towards left and the direction of ${{B}_{2}}$ will be towards right.
The magnitude of magnetic field due to a coil at a point on in its axis, at a distance of x from the its centre is given as $B=\dfrac{N{{\mu }_{0}}i{{R}^{2}}}{2{{\left( {{R}^{2}}+{{x}^{2}} \right)}^{\dfrac{3}{2}}}}$ …. (i).
Here, ${{\mu }_{0}}$ is permeability of free space, N is the number of turns of the coil, i is the current in the coil and R is the radius of the coil.
In this case, N=40, i=0.5A, R=0.5m. For coil 1, x=0 and for coil 2, x=0.1m.
Therefore,
${{B}_{1}}=\dfrac{(40)\left( 4\pi \times {{10}^{-7}} \right)(0.5){{(0.5)}^{2}}}{2{{\left( {{(0.5)}^{2}}+{{0}^{2}} \right)}^{\dfrac{3}{2}}}}=80\pi \times {{10}^{-7}}T$
And
${{B}_{2}}=\dfrac{(40)\left( 4\pi \times {{10}^{-7}} \right)(0.5){{(0.5)}^{2}}}{2{{\left( {{(0.5)}^{2}}+{{0.1}^{2}} \right)}^{\dfrac{3}{2}}}}=73.43\pi \times {{10}^{-7}}T$
Therefore, the resultant magnetic field at point O is ${{B}_{1}}-{{B}_{2}}=80\pi \times {{10}^{-7}}-73.43\pi \times {{10}^{-7}}=6.57\pi \times {{10}^{-7}}T$.
The direction of the resultant magnetic field will be in the left direction.
Similarly, the magnetic field at point O’ will be $6.57\pi \times {{10}^{-7}}T$ in the direction towards right.

Note: From the formula for the magnitude of the magnetic field due to the coil carrying current (i.e. equation (i)), we get that as we go away from the centre of the coil, on its axis, the magnitude of the magnetic field reduces. Its value is maximum at the centre of the coil.