Question

Two identical conducting spheres A and B, carry equal charge. They are separated by a distance much larger than their diameter, and the force between them is F. A third identical conducting sphere, C is uncharged. Sphere C is first touched to A, then to B, and then removed. As a result, the force between A and B would be equal to
A). $\dfrac{{3F}}{4}$
B). $\dfrac{F}{2}$
C). $F$
D). $\dfrac{{3F}}{8}$

Answer 1

Hint: For solving this question we will use Coulomb's law which is nothing but the relation between and charge on bodies and corresponding force generated. Later we will see the force on two identical spheres separated by some distance greater than its diameter.

Formula used- The force between two charges is given by
$F = \dfrac{{k{q_1}{q_2}}}{{{d^2}}}$
Where F is the force, ${q_1}\& {q_2}$ are the two charges respectively and d is the distance between them.

Complete step-by-step answer:
Coulomb's law states that the electrical force between two charged objects is directly proportional to the product of the quantity of charge on the objects and inversely proportional to the square of the separation distance between the two objects.
its scalar form, the law is:
$F = \dfrac{{k{q_1}{q_2}}}{{{d^2}}}$
Where k is Coulomb's constant ( \[k \approx 9 \times {10^9}N{m^2}{C^{ - 2}}\] ), $q_1$ and $q_2$ are the signed magnitudes of the charges, and the scalar r is the distance between the charges. The force of the interaction between the charges is attractive if the charges have opposite signs (i.e., F is negative) and repulsive if like-signed (i.e., F is positive).
Since, the initial charge on the both spheres is q

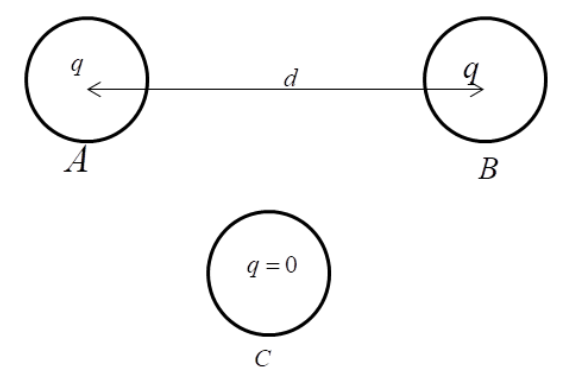
Therefore force between them is given by above formula
$F = \dfrac{{k{q_1}{q_2}}}{{{d^2}}}$
$F = \dfrac{{K{q^2}}}{{{d^2}}}...........\left( 1 \right)$
First sphere C comes in the contact of sphere A, the charge distribution will be equal

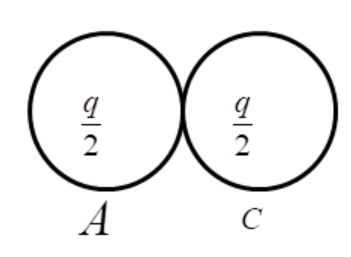
${q_c} = {q_A} = \dfrac{q}{2}$
As the sphere C comes in the contact of sphere B, the charge will distribute equally between both of them, therefore the final charge on both of them will be

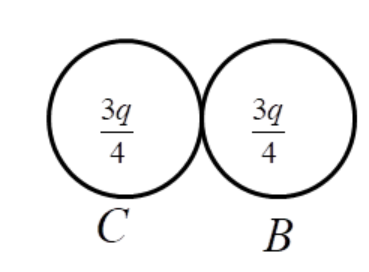
${q_c} = {q_d} = \dfrac{{q/2 + q}}{2} = \dfrac{{3q}}{4}$
Therefore the force between A and B will be given as
$
  F' = \dfrac{{K \times \dfrac{q}{2} \times \dfrac{{3q}}{4}}}{{{d^2}}} \\
  F' = \dfrac{{3F}}{8} \\
$
Hence, the correct option is “D”.

Note: Electric charge has the dimension electric current time. The SI derived unit of electric charge is the coulomb, which is defined as an ampere second whereas the force has the unit Newton. Also, two positive charges repel each other and the positive and negative charges attract each other or in general like charges repel each other and unlike charges attract each other.