Question

Two identical magnetic dipoles of magnetic moment \[1.0A{m^2}\] each, placed at a separation of 2m with their axes perpendicular to each other. The resultant magnetic field at a point midway between the dipoles is
A. $\sqrt 5 \times {10^{ - 7}}T$
B. $5 \times {10^{ - 7}}T$
C. ${10^{ - 7}}T$
D. $2 \times {10^{ - 7}}T$

Answer 1

Hint: The axial and equatorial magnetic field would be perpendicular to each other. Since these are vector quantities, We have to take their vector sum. Use the equations ${\vec B_{ax}} = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{2\vec m}}{{{r^3}}}$ and ${\vec B_{eq}} = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{2\vec m}}{{{r^3}}}$

Complete step by step answer:
We know the magnetic field at an axial point on a dipole of magnetic moment $\vec m$ is given by :
$\overrightarrow {{B_1}} = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{2\vec m}}{{{r^3}}}$ where r is the distance from centre of dipole to the axial point.
Similarly, the Magnetic field at an equatorial point, located along the perpendicular bisector of dipole is given as:
$\overrightarrow {{B_2}} = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{\vec m}}{{{r^3}}}$

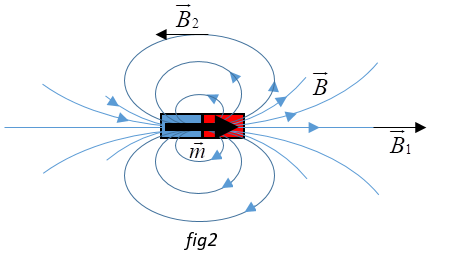
Also, the direction of $\vec B$ can easily be obtained by imagining field lines corresponding to the magnetic moment. (refer fig 2)

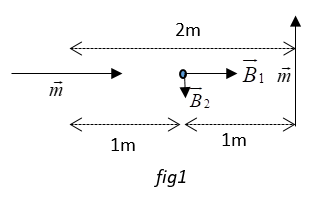
In this question, the magnetic field at point A due to the axial dipole would be a vector along the axis and that of the equatorial dipole would be perpendicular to the axis. (refer fig1)

The strength of axial field is:
$\left| {\overrightarrow {{B_1}} } \right|{\mkern 1mu} = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{2 \times 1}}{{{1^3}}} = \dfrac{{2{\mu _0}}}{{4\pi }}$

The strength of equatorial field :
\[\left| {\overrightarrow {{B_2}} } \right|\, = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{1}{{{1^3}}} = \dfrac{{{\mu _0}}}{{4\pi }}\]

Now, the net magnetic field at A would be $\overrightarrow {{B_1}} + \overrightarrow {{B_2}} $
Since these vectors are perpendicular, the net magnetic field is given by :
${B_{net}} = \sqrt {{B_1}^2 + {B_2}^2} = \dfrac{{{\mu _0}}}{{4\pi }}\sqrt {{2^2} + {1^2}} = \dfrac{{\sqrt 5 {\mu _0}}}{{4\pi }}$
So the answer is $\sqrt 5 \times {10^{ - 7}}$

Additional Information:
The magnetic moment of a magnetic substance could be defined in two ways:
If the magnetic field is a result if a known current flowing through a loop of area A
then $\vec m = I \times \vec A$
If the field is que to a permanent magnet of length L, then
$\vec m = {q_m}2\vec l$
Here ${q_m}$ is the pole strength of a magnet and unlike electric charges, ${q_m}$ does not occur isolated. It always found in pairs as $ \pm {q_m}$

Note: Though the magnetic moment vector is drawn from the south to the north pole of a magnet, it shows the same direction as that of the magnetic field. This is because, inside a magnet, magnetic fields are from south to north.