Question

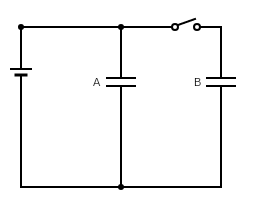
Two identified parallel plate capacitors A and B are connected to a battery of V volts with the switch S closed. The switch is now opened and the free space between the plates of the capacitors is filled with a dielectric of dielectric constant K. Find the ratio of the total electrostatic energy stored in both capacitors before and after the introduction of the dielectric.

Answer 1

Hint: It is given that when the switch is closed, there is a current V flowing through the capacitors. Find the total energy by adding up the energy contributed by each capacitor. When the switch is opened and the di-electric is filled in between, calculate the total energy in this case and find the ratio of the same.

Complete step by step answer
When switch S is closed, there is a current I flowing through the circuit which has a potential difference of V volts from the source. Energy emitted by a capacitor in this case is expressed as the product of its capacitance and the square of the voltage flowing through the capacitor. This is mathematically represented as ,
 $ \Rightarrow Q = \dfrac{1}{2}C{V^2} $ (where C is the capacitance of the capacitor and V is the voltage flowing across)
Now when switch S is closed, the total energy given out by the system is given as,
 $ \Rightarrow E = {Q_A} + {Q_B} $
Where $ {Q_A} $ is energy given out by capacitor A and $ {Q_B} $ is energy given out by capacitor B.
 $ \Rightarrow {Q_A} = {Q_B} = \dfrac{1}{2}C{V^2} $
The overall energy can be written as ,
 $ \Rightarrow E = C{V^2} $
Now, when the switch is open and the di-electric of di-electric constant K is inserted between the parallel plate capacitors, there will be a flow of voltage V across the capacitor A. Whereas in capacitor B the stored voltage will be flowing across the plates, which is denoted by $ {V'} $ . Now , total energy of the system is again the sum of the individual energy possessed by the capacitors
 $ \Rightarrow {E'} = {Q_A} + {Q_B} $
Now, energy across the capacitor A is given as,
 $ \Rightarrow {Q_A} = \dfrac{1}{2}(KC){V^2} $ , Where K is the di-electric constant.
In case of capacitor B, the voltage flowing across the plates will be the stored voltage $ {V'} $ . This can be represented as $ {V'} = \dfrac{V}{K} $ . Using this, the energy across capacitor B is,
 $ \Rightarrow {Q_B} = \dfrac{1}{2}(KC)V{'^2} $
On substituting and cancelling the common term, we get,
 $ \Rightarrow {Q_B} = \dfrac{1}{2}\dfrac{{C{V^2}}}{K} $
Now total energy $ {E'} $ is given as,
 $ \Rightarrow {E'} = {Q_A} + {Q_B} $
On substituting ,
 $ \Rightarrow {E'} = \dfrac{1}{2}KC{V^2} + \dfrac{1}{2}\dfrac{{C{V^2}}}{K} $
Taking the common term, we get,
 $ \Rightarrow {E'} = \dfrac{1}{2}C{V^2}(K + \dfrac{1}{K}) $
On simplifying, we get,
 $ \Rightarrow {E'} = \dfrac{1}{2}C{V^2}(\dfrac{{{K^2} + 1}}{K}) $
Now, the ratio between the first and second case is given as ,
 $ \Rightarrow \dfrac{E}{{{E'}}} = \dfrac{{C{V^2}}}{{\dfrac{1}{2}C{V^2}(\dfrac{{{K^2} + 1}}{K})}} $
On removing the common term and taking the denominator term to numerator , we get,
 $ \Rightarrow \dfrac{E}{{{E'}}} = \dfrac{{2K}}{{{K^2} + 1}} $
Hence, the ratio of the total electrostatic energy stored in both capacitors before and after introduction of di-electric is found out.

Note
In a parallel plate capacitor setup, the capacitance depends upon the charge flowing between the plate and the Voltage applied through the circuit, the area between the plate and the permissibility factor.