
Two inductors each of inductance L are connected in parallel. One more inductor of value 5mH is connected in a series of this configuration then the effective inductance is 15 mH. The value of L is ---- mH.
A. 10
B. 5.0
C. 2.5
D. 20
Answer
504k+ views
Hint: Find the effective inductance of the inductance in parallel in terms of L and then find the value of the effective inductance after the addition of the one more inductor using the formulae of the effective inductance in case of series and parallel inductors.
Complete step by step solution:
Now we know the value of the effective inductance when the inductors are in parallel is given as
We get the value of the effective inductance in case of the inductors arranged in series as:
We now can solve the problem quickly, first we will draw a diagram for the situation given:
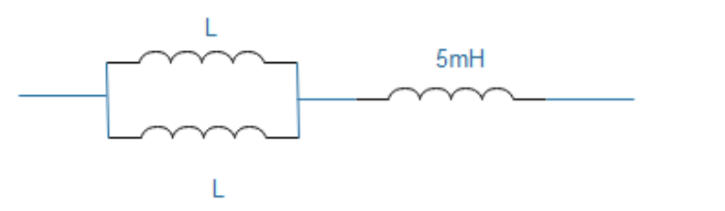
We can now implement the above formula to get the value of effective inductance:
We are given that the two inductance of value L are connected in parallel so the effective value of inductance
So, we get
Now we have found the effective value of the one part of the circuit we get the value of the final effective value of the inductance by adding the value connected in series
So, we get
We are given the effective value of the combination as 15 mH
So we get the value of the L by equating the above as below:
We get that
We get
L = 20 mH
Hence, we found the effective value of the inductance and then found the required value of L as 20 mH.
Note: The effective value of the inductance can be calculated in a similar fashion as we do calculate in case of resistors but it is not the same case in case of capacitors. For the capacitors, we use the parallel form for the effective series resistance series form for the effective parallel capacitance.
So, we need to take care of that if we are given a combination of capacitors.
Complete step by step solution:
Now we know the value of the effective inductance when the inductors are in parallel is given as
We get the value of the effective inductance in case of the inductors arranged in series as:
We now can solve the problem quickly, first we will draw a diagram for the situation given:

We can now implement the above formula to get the value of effective inductance:
We are given that the two inductance of value L are connected in parallel so the effective value of inductance
So, we get
Now we have found the effective value of the one part of the circuit we get the value of the final effective value of the inductance by adding the value connected in series
So, we get
We are given the effective value of the combination as 15 mH
So we get the value of the L by equating the above as below:
We get that
We get
L = 20 mH
Hence, we found the effective value of the inductance and then found the required value of L as 20 mH.
Note: The effective value of the inductance can be calculated in a similar fashion as we do calculate in case of resistors but it is not the same case in case of capacitors. For the capacitors, we use the parallel form for the effective series resistance series form for the effective parallel capacitance.
So, we need to take care of that if we are given a combination of capacitors.
Latest Vedantu courses for you
Grade 11 Science PCM | CBSE | SCHOOL | English
CBSE (2025-26)
School Full course for CBSE students
₹41,848 per year
Recently Updated Pages
Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Class 12 Question and Answer - Your Ultimate Solutions Guide

Master Class 12 Economics: Engaging Questions & Answers for Success

Trending doubts
Give 10 examples of unisexual and bisexual flowers

Draw a labelled sketch of the human eye class 12 physics CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE

What are the major means of transport Explain each class 12 social science CBSE

Draw a diagram of a flower and name the parts class 12 biology ICSE




