
Two inductors
Answer
493.2k+ views
1 likes
Hint: At the time when the current starts flowing, we will have a minimum current at
Complete step by step answer:
At time
At
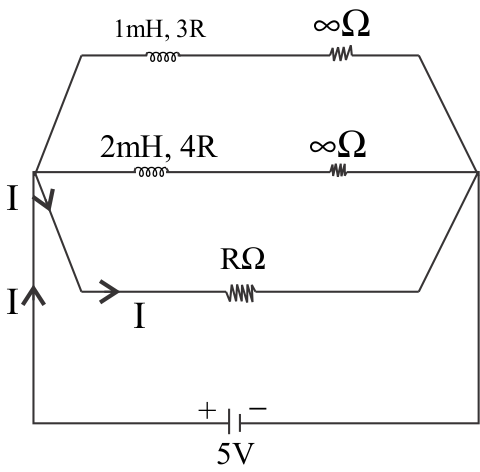
In reality, we don’t have resistances of infinite ohm with both inductors, but for visualization, both inductors will be acting as resistances of infinite ohm and there will be no current passing through them.
So using ohm’s law
After a long time, inductors will not resist anymore, the only resistance will be due to their internal resistance and
After long time, equivalent circuit will be like this:
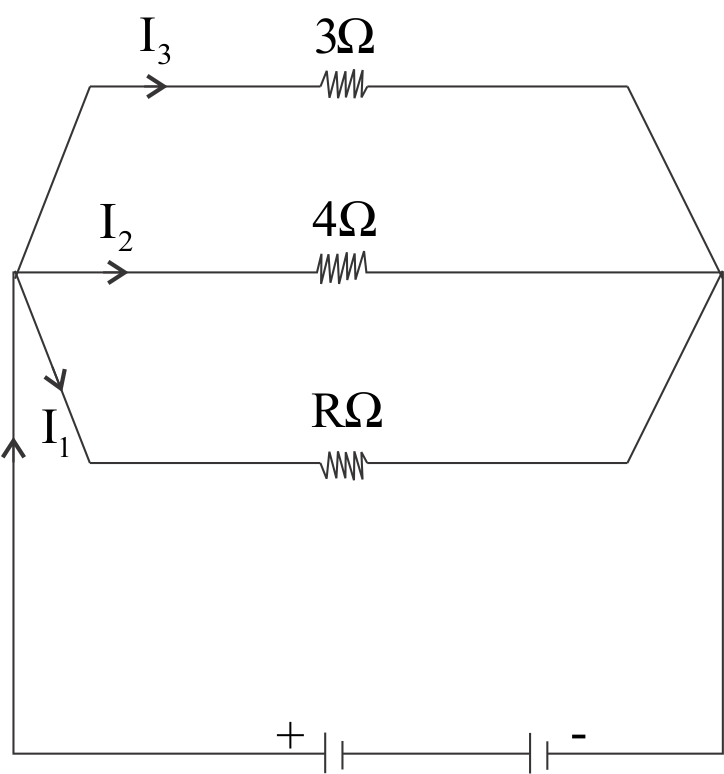
After a long time, resistance through inductors will only be due to their internal resistances and current will easily pass through them.
At that time, the equivalent resistance,
On solving the above equation, we get,
On solving this, we get equivalent resistance as,
Now applying ohm’s law on
Required value
So our answer is 8.
Note: At time
Complete step by step answer:
At time
At

In reality, we don’t have resistances of infinite ohm with both inductors, but for visualization, both inductors will be acting as resistances of infinite ohm and there will be no current passing through them.
So using ohm’s law
After a long time, inductors will not resist anymore, the only resistance will be due to their internal resistance and
After long time, equivalent circuit will be like this:

After a long time, resistance through inductors will only be due to their internal resistances and current will easily pass through them.
At that time, the equivalent resistance,
On solving the above equation, we get,
On solving this, we get equivalent resistance as,
Now applying ohm’s law on
Required value
So our answer is 8.
Note: At time
Latest Vedantu courses for you
Grade 10 | CBSE | SCHOOL | English
Vedantu 10 CBSE Pro Course - (2025-26)
School Full course for CBSE students
₹37,300 per year
Recently Updated Pages
Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Class 12 Question and Answer - Your Ultimate Solutions Guide

Master Class 11 Economics: Engaging Questions & Answers for Success

Trending doubts
Draw a labelled sketch of the human eye class 12 physics CBSE

a Tabulate the differences in the characteristics of class 12 chemistry CBSE

Which one of the following is a true fish A Jellyfish class 12 biology CBSE

Why is the cell called the structural and functional class 12 biology CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Write the difference between solid liquid and gas class 12 chemistry CBSE




