Question

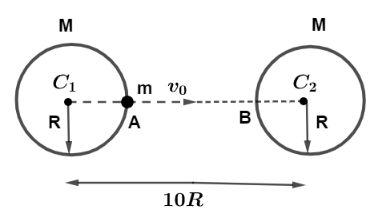
Two large spherical objects of mass M each are fixed as shown in figure. A small point mass $m$ is projected from point $A$ heading towards the centre ${C_2}$ of the second sphere. The minimum velocity of point mass so that it can reach up to second object at point $B$ is $\dfrac{n}{3}\sqrt {\dfrac{{GM}}{{5R}}} $ then, calculate $n$ (Neglect other Gravitational forces)

Answer 1

Hint:In order to solve the given question, we will use the concept of conservation of energy, in the given case we will neglect any other form of energy except gravitational potential energy and kinetic energy of point mass. We will find the minimum velocity of point mass m.

Formula used:
Conservation of energy which can be written as
(Gravitational Potential energy $ + $ Kinetic energy) at point $A$ $ = $ (Potential energy $ + $ Kinetic energy) at point $B$.
Gravitational potential energy between two bodies is given by,
$P.E = - \dfrac{{G{M_1}{M_2}}}{R}$
Kinetic energy of a body is written as $K.E = \dfrac{1}{2}m{v^2}$.

Complete step by step answer:
From the given diagram we can see that, let us find the $P.E\,(and)\,K.E$ at point $A$.
Since two spherical objects will have a potential energy of $ - \dfrac{{G{m^2}}}{{10R}}$
Sphere $B$ and point mass $m$ will have a potential energy of $ - \dfrac{{GMm}}{{9R}}$
Sphere $A$ and point mass $m$ will have a potential energy of $ - \dfrac{{GMm}}{R}$
Kinetic energy of point mass at point $A$ will be $\dfrac{1}{2}m{v^2}$
Now, total energy of the system at point $A$ is the sum of all above energies, which can be written as
${E_A} = - (\dfrac{{G{m^2}}}{{10R}} + \dfrac{{GMm}}{{9R}} + \dfrac{{GMm}}{R}) + \dfrac{1}{2}m{v^2}$
$\Rightarrow {E_A} = - \dfrac{{G{m^2}}}{{10R}} - \dfrac{{10GMm}}{{9R}} + \dfrac{1}{2}m{v^2}$

Now, taking point $B$ we will have, kinetic energy will be zero as point mass will came to rest only potential energy will act at point $B$ will be due to point mass and other two spheres which we already found as;
Sphere $B$ and point mass $m$ will have a potential energy of $ - \dfrac{{GMm}}{{9R}}$
Sphere $A$ and point mass $m$ will have a potential energy of $ - \dfrac{{GMm}}{R}$
So, total energy at point $B$ can be written as
${E_B} = - \dfrac{{10GMm}}{{9R}}$

So, equate both equations ${E_A} = {E_B}$ we get,
$ - \dfrac{{G{m^2}}}{{10R}} - \dfrac{{10GMm}}{{9R}} + \dfrac{1}{2}m{v^2} = - \dfrac{{10GMm}}{{9R}}$
$\Rightarrow \dfrac{{G{m^2}}}{{10R}} = \dfrac{1}{2}m{v^2}$
$\Rightarrow \dfrac{{Gm}}{{5R}} = {v^2}$
$\Rightarrow v = \sqrt {\dfrac{{GM}}{{5R}}} $
Compare this value with given relation $\dfrac{n}{3}\sqrt {\dfrac{{GM}}{{5R}}} $
So, $\dfrac{n}{3}\sqrt {\dfrac{{GM}}{{5R}}} = \sqrt {\dfrac{{GM}}{{5R}}} $
So, $n = 3$

Hence, $n = 3$ is the required value.

Note:It should be remembered that, as the point mass object reaches to the surface of another sphere at point $B$ it will came to rest and hence its Kinetic energy is taken as zero whereas potential energy is always due to work done by the body against the gravity and hence always taken as negative.