
Two objects of masses 100g and 200g are moving along the same line and direction with velocities
A)
B)
C)
D)
Answer
498.3k+ views
Hint: Collision is short-duration interaction between two bodies or more than two bodies simultaneously causing a change in motion of bodies. Collision is of three types:
(i) Perfectly elastic collision.
(ii) Inelastic collision.
(iii) Perfectly inelastic collision.
To solve this type of question we use the law of conservation of momentum.
Complete step by step answer:
Given,
We have to find the velocity of the first object
Flowing is the diagram showing the situation.
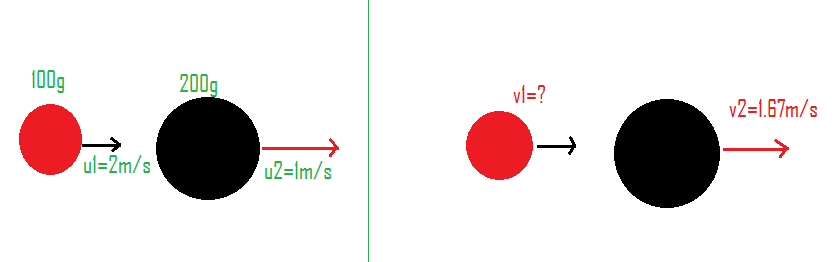
Now let us use the concept of conservation of linear momentum which states that the total initial momentum is equal to the total final momentum.
Initial momentum = Final momentum
Let us write the linear momentum of the system before the collision.
Let us now substitute the values.
Let us simplify it.
Let us write the linear momentum of the system after the collision.
Let us now substitute the values.
Let us simplify it.
Now using linear momentum conservation, let us equate equation (1) and (2).
Let us simplify it.
Note:
There are two types of collisions between two bodies as given below:
1) Head-on collisions (also known as one-dimensional collisions) – In this type of collision, the velocity of each body just before impact is along the line of impact after collision also.
2) Non-head-on collisions, (also known as two-dimensional collisions) – In this type of collision, the velocity of each body just before impact is not along the line of impact after the collision.
(i) Perfectly elastic collision.
(ii) Inelastic collision.
(iii) Perfectly inelastic collision.
To solve this type of question we use the law of conservation of momentum.
Complete step by step answer:
Given,
We have to find the velocity of the first object
Flowing is the diagram showing the situation.

Now let us use the concept of conservation of linear momentum which states that the total initial momentum is equal to the total final momentum.
Initial momentum = Final momentum
Let us write the linear momentum of the system before the collision.
Let us now substitute the values.
Let us simplify it.
Let us write the linear momentum of the system after the collision.
Let us now substitute the values.
Let us simplify it.
Now using linear momentum conservation, let us equate equation (1) and (2).
Let us simplify it.
Note:
There are two types of collisions between two bodies as given below:
1) Head-on collisions (also known as one-dimensional collisions) – In this type of collision, the velocity of each body just before impact is along the line of impact after collision also.
2) Non-head-on collisions, (also known as two-dimensional collisions) – In this type of collision, the velocity of each body just before impact is not along the line of impact after the collision.
Recently Updated Pages
Express the following as a fraction and simplify a class 7 maths CBSE

The length and width of a rectangle are in ratio of class 7 maths CBSE

The ratio of the income to the expenditure of a family class 7 maths CBSE

How do you write 025 million in scientific notatio class 7 maths CBSE

How do you convert 295 meters per second to kilometers class 7 maths CBSE

Write the following in Roman numerals 25819 class 7 maths CBSE

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

What are Quantum numbers Explain the quantum number class 11 chemistry CBSE

Write the differences between monocot plants and dicot class 11 biology CBSE

Who built the Grand Trunk Road AChandragupta Maurya class 11 social science CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light




