Question

Two parallel infinite line charges with linear charge densities $+\lambda \,C/m$and $-\lambda \,C/m$ are placed at a distance of $2R$ in free space. What is the electric field midway between the two-line charges?
$\begin{align}
  & A.\,\,Zero \\
 & B.\,\,\dfrac{2\lambda }{\pi {{\varepsilon }_{0}}R}N/C \\
 & C.\,\,\dfrac{\lambda }{\pi {{\varepsilon }_{0}}R}N/C \\
 & D.\,\,\dfrac{\lambda }{2\pi {{\varepsilon }_{0}}R}N/C \\
\end{align}$

Answer 1

Hint: Electric field for a line charge can be calculated using Coulomb’s Law, which can help to get the electric force between the two line charges and since the details regarding the linear charge densities and the distance between them are given, then to get the net electric field between the two-line charges, we just need to add the electric field of both line charges individually.

Formula used:
$Electric\,Field(E)=\dfrac{\lambda }{\pi {{\varepsilon }_{0}}d}$

Complete step by step answer:
According to the question, the magnitude of the charge density is $\lambda \,C/m$ and the distance between the two line charges is given, which means $d=2R$, the given scenario is depicted in the diagram shown below.

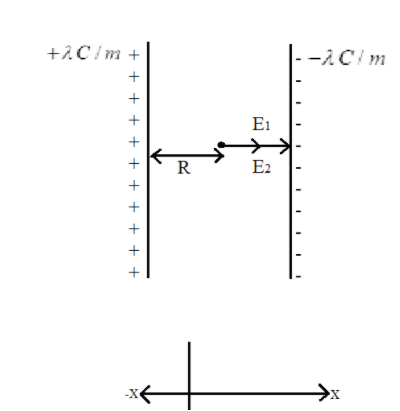
So, the electric field due to line charge $(1)$ is:
${{E}_{1}}=\dfrac{\lambda }{\pi {{\varepsilon }_{0}}(2R)}N/C$
And, the electric field due to line charge $(2)$ is:
${{E}_{2}}=\dfrac{\lambda }{\pi {{\varepsilon }_{0}}(2R)}N/C$
Hence, the electric field mid-way between the two-line charges can be written as:
${{E}_{net}}={{E}_{1}}+{{E}_{2}}$
Substituting the value of both the line charge electric field, we get:
$\begin{align}
  & \Rightarrow {{E}_{net}}=(\dfrac{\lambda }{2\pi {{\varepsilon }_{0}}R}+\dfrac{\lambda }{2\pi {{\varepsilon }_{0}}R})N/C \\
 & \therefore {{E}_{net}}=\dfrac{\lambda }{\pi {{\varepsilon }_{0}}R}N/C \\
\end{align}$

Note:
It’s better to construct a diagram for the details given in the question, which helps to understand the problem easily and also shows a way of getting the solution. In this question, after marking the details given in a diagram, it was easy to find the net electric field by just placing the values in the formula.