Question

Two particles of masses $4kg$ and $6kg$ are at rest, separated by $20m$. If they move towards each other under mutual force of attraction, the position of the point where they meet is
$A)12m$ from $4kg$ body
$B)12m$ from $6kg$ body
$C)8m$ from $4kg$ body
$D)10m$ from $4kg$ body

Answer 1

Hint: Since no other external forces are acting on the given masses except a mutual force of attraction, the concept of centre of mass can be used here. From the expression derived with respect to the centre of mass of the system, we can determine the position of meeting easily.
Formula used:
${{m}_{1}}{{r}_{1}}={{m}_{2}}{{r}_{2}}$

Complete answer:
We are provided with two particles of masses $4kg$ and $6kg$, at rest, separated by a distance $20m$. If they start moving towards each other under mutual force of attraction, we are required to determine the position of the point where they meet.
Firstly, let us call the $4kg$ mass, ${{m}_{1}}$ and the $6kg$ mass, ${{m}_{2}}$. Also, let us call the distance of separation between these masses, $r$. Clearly,
$\begin{align}
  & {{m}_{1}}=4kg \\
 & {{m}_{2}}=6kg \\
 & r=20m \\
\end{align}$
Now, we are told that both ${{m}_{1}}$ and ${{m}_{2}}$ start moving towards each other due to a mutual force of attraction. Clearly, there is no external force acting on the system and hence, we can use the concept of centre of mass, to proceed.
If ${{r}_{1}}$ represents the distance from ${{m}_{1}}$ and if ${{r}_{2}}$ represents the distance from ${{m}_{2}}$, at which both ${{m}_{1}}$ and ${{m}_{2}}$ meet, then, using the concept of centre of mass, we have
${{m}_{1}}{{r}_{1}}={{m}_{2}}{{r}_{2}}$
Let this be equation 1.

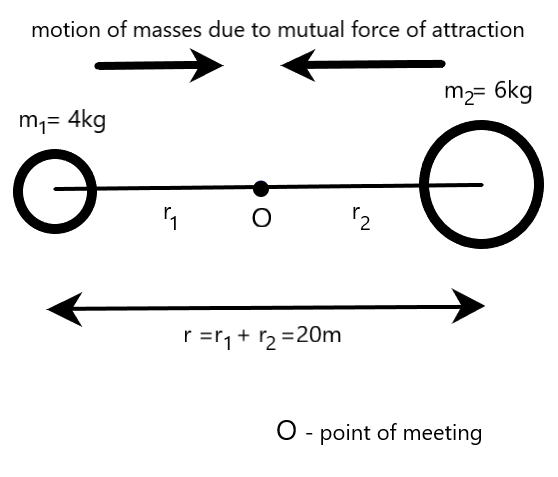
From the figure given above, it is also clear that
$r={{r}_{1}}+{{r}_{2}}=20m$
Let this be equation 2.
Now, substituting equation 2 in equation 1, we have
${{m}_{1}}{{r}_{1}}={{m}_{2}}(20-{{r}_{1}})\Rightarrow {{m}_{1}}{{r}_{1}}+{{m}_{2}}{{r}_{1}}=20{{m}_{2}}\Rightarrow {{r}_{1}}=\dfrac{20{{m}_{2}}}{{{m}_{1}}+{{m}_{2}}}$
Let this be equation 3.
Substituting the values of ${{m}_{1}}$ and ${{m}_{2}}$ in equation 3, we have
${{r}_{1}}=\dfrac{20{{m}_{2}}}{{{m}_{1}}+{{m}_{2}}}=\dfrac{20\times 6}{4+6}=\dfrac{120}{10}=12m$
Therefore, under mutual force of attraction, the position of the point where both masses ${{m}_{1}}=4kg$ and ${{m}_{2}}=6kg$ meet is equal to ${{r}_{1}}=12m$ from ${{m}_{1}}=4kg$ mass.

So, the correct answer is “Option A”.

Note:
Students need to be clear with the concept of centre of mass. Centre of mass of a system of mass distribution is a unique point at which, the product of each mass and its respective position, relative to the unique point, sums up to be zero. To put in simple language, the centre of mass of a mass distribution is a point at the centre of the distribution, where the total mass of the distribution is supposed to be concentrated.