
Two plane mirrors arranged at right angles to each other as shown in figure A. A ray of light is incident on the horizontal mirror at an angle
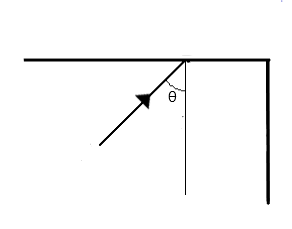
(A)
(B)
(C)
(D) All of these

Answer
482.4k+ views
3 likes
Hint
For parallel emergent ray, the angle which the incident ray makes with the vertical (normal of horizontal mirror) must be equal to the angle of which the emergent ray (second reflected ray) makes with the vertical (surface of second mirror). Angle of reflection is equal to angle of incidence. So by using this we can calculate the answer.
Formula used: In the solution we will be using the following formula,
Complete step by step answer
In the question we are given the incident ray in the diagram. So on completing the figure we get,
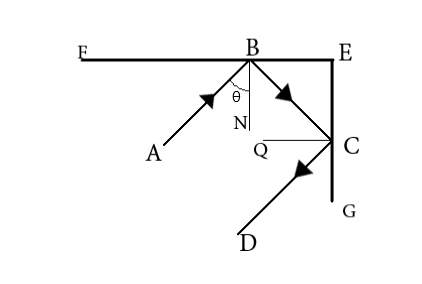
The incoming incident ray AB has an angle
Hence from diagram angle
Thus, in general, angle
From a rule of geometry, alternate angles are equal. Therefore, the angles
Since
The line QC is the normal of the mirror EG, hence angle
Then
Replacing
Now, we see that the line BC which is the reflected ray of mirror FE is the incident ray of mirror EG. Hence,
Also, in a vertical plane mirror, the angle of incidence is equal to the angle of reflection.
Hence,
Then, in total,
Line
Hence, angle
Evaluating, we have the value as,
So we get,
We see that irrespective of incident angle
Thus, the correct option is (D).
Note
A common error is for students to think that because ray AB is parallel to ray DC, the shape ABCD must be part of a rectangle. However, this is erroneous. To circumvent such error, we need to think as follows: if angle
For parallel emergent ray, the angle which the incident ray makes with the vertical (normal of horizontal mirror) must be equal to the angle of which the emergent ray (second reflected ray) makes with the vertical (surface of second mirror). Angle of reflection is equal to angle of incidence. So by using this we can calculate the answer.
Formula used: In the solution we will be using the following formula,
Complete step by step answer
In the question we are given the incident ray in the diagram. So on completing the figure we get,

The incoming incident ray AB has an angle
Hence from diagram angle
Thus, in general, angle
From a rule of geometry, alternate angles are equal. Therefore, the angles
Since
The line QC is the normal of the mirror EG, hence angle
Then
Replacing
Now, we see that the line BC which is the reflected ray of mirror FE is the incident ray of mirror EG. Hence,
Also, in a vertical plane mirror, the angle of incidence is equal to the angle of reflection.
Hence,
Then, in total,
Line
Hence, angle
Evaluating, we have the value as,
So we get,
We see that irrespective of incident angle
Thus, the correct option is (D).
Note
A common error is for students to think that because ray AB is parallel to ray DC, the shape ABCD must be part of a rectangle. However, this is erroneous. To circumvent such error, we need to think as follows: if angle
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Give 10 examples of unisexual and bisexual flowers

Draw a labelled sketch of the human eye class 12 physics CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE

What are the major means of transport Explain each class 12 social science CBSE

Why is the cell called the structural and functional class 12 biology CBSE




