Question

Two point charges $ 4 \times {10^{ - 6}}C $ and $ 2 \times {10^{ - 6}}C $ are placed at the vertices $ A $ and $ B $ of a right angled triangle $ ABC $ respectively. $ B $ is the right angle, $ AC = 2 \times {10^{ - 2}}m $ and $ BC = {10^{ - 2}}m $ . Find the magnitude and direction of resultant electric intensity at $ C $ ?

Answer 1

Hint: To solve this question first we will draw the diagram and we will find the electric field at point $ A $ by using the formula and similarly at point $ B $ after that we will find the angle $ \theta $ because without $ \theta $ we will not be able to find the resultant magnitude and then we will use the vector sum to find the net resultant and after to find the direction means we have to find $ \tan \alpha $ after finding we will get our required solution.
Magnitude of the electric field is given by:
 $ E = \dfrac{{kq}}{{{r^2}}} $
Where,
 $ k $ is electrostatic constant and its value is $ 9 \times {10^9} $ ,
 $ q $ is the charge and
 $ r $ is the distance.

Complete answer:

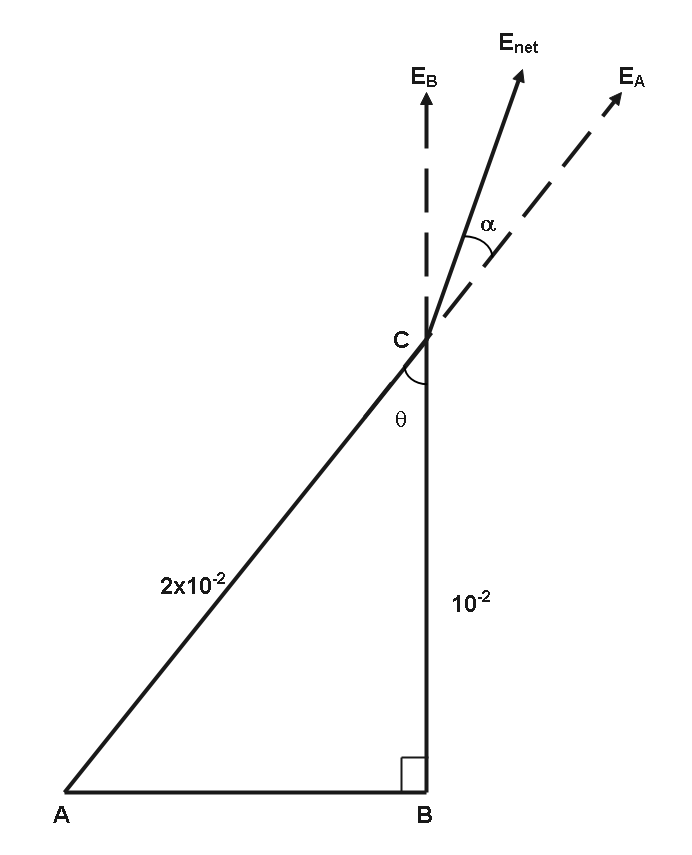
According to the question,
Charge at point $ A $ is $ 4 \times {10^{ - 6}}C $ and
Charge at point $ B $ is $ 2 \times {10^{ - 6}}C $ .
Length, $ AC = 2 \times {10^{ - 2}}m $ and
Length, $ BC = {10^{ - 2}}m $ .
So, the electric field at point $ A $ is given by,
 $ E = \dfrac{{kq}}{{{r^2}}} $
Now, substituting the above given values and solving,
 $
  {E_A} = \dfrac{{9 \times {{10}^9} \times 4 \times {{10}^{ - 6}}}}{{{{\left( {2 \times {{10}^{ - 2}}m} \right)}^2}}} \\
   \Rightarrow {E_A} = \dfrac{{9 \times {{10}^9} \times 4 \times {{10}^{ - 6}}}}{{4 \times {{10}^{ - 4}}}} \\
   \Rightarrow {E_A} = 9 \times {10^7}N{\text{ }}{C^{ - 1}} \\
  $
Similarly, the electric field at point $ B $ is given by,
 $ E = \dfrac{{kq}}{{{r^2}}} $
Now, substituting the above given values and solving,
 $
  {E_B} = \dfrac{{9 \times {{10}^9} \times 2 \times {{10}^{ - 6}}}}{{{{\left( {{{10}^{ - 2}}m} \right)}^2}}} \\
   \Rightarrow {E_B} = \dfrac{{9 \times {{10}^9} \times 2 \times {{10}^{ - 6}}}}{{{{10}^{ - 4}}}} \\
   \Rightarrow {E_B} = 18 \times {10^7}N{\text{ }}{C^{ - 1}} \\
  $
Now, we have to calculate the magnitude of resultant electric intensity at $ C $
To find this first we have to find the angle $ \theta $ .
In $ \vartriangle ABC $
 $ \cos \theta = \dfrac{{{{10}^{ - 2}}}}{{2 \times {{10}^{ - 2}}}} = \dfrac{1}{2} $
And we know that, $ \cos {60^ \circ } = \dfrac{1}{2} $
Therefore, $ \theta = {60^ \circ } $
Now, applying vector law of addition to find the magnitude,
 $ E = \sqrt {{E_A} + {E_B} + 2{E_A}{E_B}\cos \theta } $
Now, substituting all the values in above formula,
 $
  E = \sqrt {{E_A} + {E_B} + 2{E_A}{E_B}\cos \theta } \\
   \Rightarrow E = \sqrt {{{\left( {9 \times {{10}^7}} \right)}^2} + {{\left( {18 \times {{10}^7}} \right)}^2} + \left\{ {2 \times 9 \times {{10}^7} \times 18 \times {{10}^7}\left( {\dfrac{1}{2}} \right)} \right\}} \\
   \Rightarrow E = \sqrt {81 \times {{10}^{14}} + 324 \times {{10}^{14}} + 162 \times {{10}^{14}}} \\
  $
On further solving,
 $
  E = \sqrt {81 \times {{10}^{14}} + 324 \times {{10}^{14}} + 162 \times {{10}^{14}}} \\
   \Rightarrow E = \sqrt {547 \times {{10}^{14}}} \\
   \Rightarrow E = 2.38 \times {10^8}N{\text{ }}{C^{ - 1}} \\
  $
So, the magnitude of resultant electric intensity at $ C $ is $ 2.38 \times {10^8}N{\text{ }}{C^{ - 1}} $ .
Now, we have to find the direction of the electric field at point $ C $ .
Which, is nothing but $ \tan \alpha $
And is given by,
 $ \tan \alpha = \dfrac{{{E_B}\sin \theta }}{{{E_A} + {E_B}\cos \theta }} $
Now, substituting the values and solving we get,
 $
  \tan \alpha = \dfrac{{18 \times {{10}^7}\sin {{60}^ \circ }}}{{9 \times {{10}^7} + 18 \times {{10}^7}\cos {{60}^ \circ }}} \\
   \Rightarrow \tan \alpha = \dfrac{{18 \times {{10}^7} \times \dfrac{{\sqrt 3 }}{2}}}{{9 \times {{10}^7} + 9 \times {{10}^7}}} \\
   \Rightarrow \tan \alpha = \dfrac{{\sqrt 3 }}{2} \\
   \Rightarrow \alpha = {40.9^ \circ } \\
  $
Hence, the magnitude and direction of resultant electric intensity at $ C $ is $ 2.38 \times {10^8}N{\text{ }}{C^{ - 1}} $ and $ {40.9^ \circ } $ respectively.

Note:
It's important to remember that the electric field is defined as the force per unit of charge. Coulomb's Law states that the force between two charged particles is directly proportional to the charges and inversely proportional to the square of the distance between the charged particles, hence this value of electric field can be calculated. Keep in mind that in the case of positive charge, the electric field is radially outward, whereas in the case of negative charge, it is radially inward.