Question

Two poles of opposite height are standing opposite to each other, on either side of a road which is 80 m wide. From a point between them from the road, the angle of elevation of the top of the poles is ${{60}^{o}},{{30}^{o}}$ respectively .Find the height of the poles.

Answer 1

Hint: We have to consider a point P such that the distance of the poles from point P are x and (80-x) respectively. Then applying the formula of tanθ we can find the value of x.
So here we are given 2 poles which have identical heights. They are separated by a road of width 80 m. There is a point from which the angle of elevation of the poles is ${{60}^{o}},{{30}^{o}}$respectively.

Complete step-by-step answer:

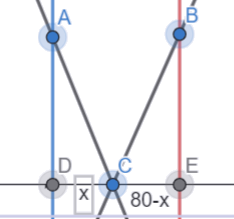
Let us consider AD and BE are the poles of identical height. Let us consider C be the point in the road such that $\angle ACD={{60}^{o}}$ and $\angle BCE={{30}^{o}}$
Let us consider the distance CD be x. So the distance CE = 80-x as the total distance is 80.
Let us consider the height of the poles be h.
In △ ADC,
DC = x, AD = h, $\angle ACD={{60}^{o}}$
We know, $\tan \theta =\dfrac{\text{perpendicular}}{\text{base}}$
$\begin{align}
  & \Rightarrow \tan (60{}^\circ )=\dfrac{h}{x} \\
 & \Rightarrow \sqrt{3}=\dfrac{h}{x} \\
 & \Rightarrow h=\sqrt{3}x..........(i) \\
\end{align}$
In △ BCE,
CE =80- x, AD = h, $\angle BCE={{30}^{o}}$
We know, $\tan \theta =\dfrac{\text{perpendicular}}{\text{base}}$
$\begin{align}
  & \tan (30{}^\circ )=\dfrac{h}{80-x} \\
 & \Rightarrow \dfrac{1}{\sqrt{3}}=\dfrac{h}{80-x} \\
 & \Rightarrow 80-x=h\sqrt{3} \\
 & \Rightarrow h=\dfrac{80-x}{\sqrt{3}}........(ii) \\
\end{align}$
Equating equation (i) and (ii), we get
$\sqrt{3}x=\dfrac{80-x}{\sqrt{3}}$
$\Rightarrow 3x=80-x$
$\Rightarrow 4x=80$
$\Rightarrow x=20$
From equation (i), we get
$h=\sqrt{3}x$
Substituting the value of ‘x’, we get
$h=1.732\times 20=34.64m$
Therefore, the height of the pole is 34.64m.
Note: It is suggested to take the distance between the point and two poles as x and 80-x respectively. Instead if x and y was taken the question would become unnecessarily complicated and chances of error would increase.