Question

Two ships are sailing in the sea on the two sides of a lighthouse. The angle of elevation of the top of the lighthouse observed from the ships are $ {{30}^{\circ }} $ and $ {{45}^{\circ }} $ respectively. If the lighthouse is 100 m high, the distance between the two ships is: \[\]
A. 173 m\[\]
B. 200 m \[\]
C. 273 m\[\]
D. 300 m\[\]

Answer 1

Hint: We designate A as the top of the light house, D as the bottom of the light house. We denote B and C as the position of the ships. We take tangent of the angles of elevation $ \angle ABD={{30}^{\circ }},\angle ACD={{45}^{\circ }} $ in the triangles ABD and ACD to find BD and CD. We find the distance between the ships $ BC=BD+CD $ .\[\]

Complete step-by-step answer:

We know that angle of elevation is the angle formed at the eye of the observer by the line of sight towards an object and the horizontal line with the condition that the object is above the horizontal line. \[\]

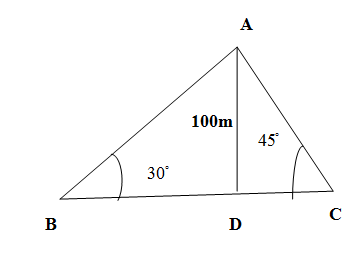
Let AD be the lighthouse with A as the top lighthouse and D as the bottom of the lighthouse. AD is the height of a lighthouse. Let B and C be the position of two ships sailing in the sea on the two sides of a lighthouse. We are asked to find the question distance between ships BC. \[\]
 The observer at the ship positioned at B sees the top A with respect to the horizontal line BD subtends the angle of elevation $ \angle ABD $ . Similarly, the observer at the ship positioned at C sees the top A with respect to the horizontal line CD subtends the angle of elevation $ \angle ACD $ . We are given in the question that
\[\angle ABD={{30}^{\circ }},\angle ACD={{45}^{\circ }},AC=100\text{m}\]
The tangent of the angle is the ratio of opposite side to the adjacent side (excluding hypotenuse) in right angled triangle. We have in the right angled triangle ABD,
\[\begin{align}
  & \tan \left( \angle ABD \right)=\dfrac{AD}{BD} \\
 & \Rightarrow \tan {{30}^{\circ }}=\dfrac{100}{BD} \\
 & \Rightarrow BD=\dfrac{100}{\tan {{30}^{\circ }}}=100\times \sqrt{3}=100\sqrt{3}\text{m} \\
\end{align}\]
We have in the right angled triangle ACD,
\[\begin{align}
  & \tan \left( \angle ACD \right)=\dfrac{AD}{CD} \\
 & \Rightarrow \tan {{45}^{\circ }}=\dfrac{100}{BD} \\
 & \Rightarrow BD=\dfrac{100}{\tan {{45}^{\circ }}}=\dfrac{100}{1}=100\text{m} \\
\end{align}\]
So the distance between the ships is
\[ BC=BD+CD=100\text{+100}\sqrt{3}=100+100\times 1.73=273\text{m} \]
So the correct option is C. \[\]

So, the correct answer is “Option C”.

Note: We can alternatively assign $ \angle ABD={{45}^{\circ }},\angle ACD={{30}^{\circ }} $ to solve the problem. We must be careful of the confusion between angle of elevation and depression where the object lies below the horizontal line. All vertical objects flags, trees, towers subtend angle of elevation but all objects below the ground like fish, sunken ships, metal ores subtend angle of depression.