
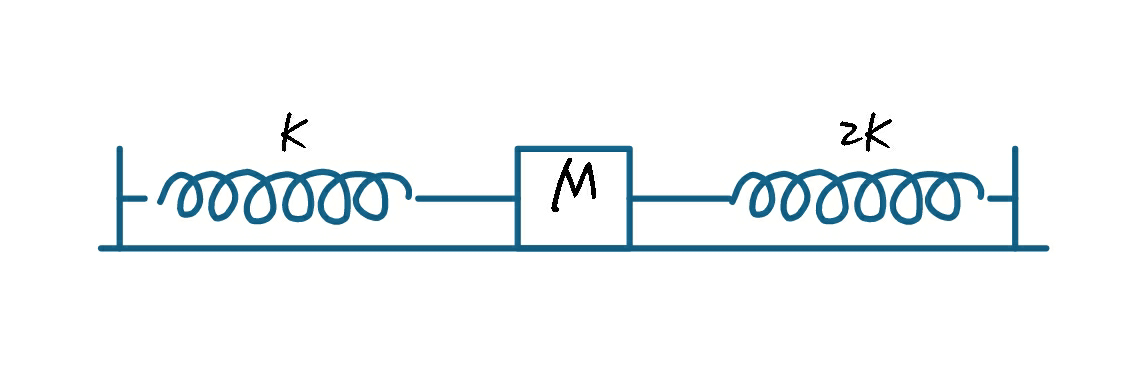
Two springs are connected in series and the combination is pulled by a constant force. If spring constant of two springs are $ $K\text{ and 2}K$ , then the ratio of potential energy stored in the springs is
Answer
143.7k+ views
Hint We know that PE is the amount of energy started at the highest point.
Here, two springs are converted in series
Therefore, using $P.E=\dfrac{1}{2}{{K}_{2}}$
Complete Step by Step Solution
$2:1$
For spring ${{S}_{1}}\text{ the spring constant is }K$
For spring${{S}_{2}}$ the spring constant is $2K$
Now, applying the potential energy formula for spring ${{S}_{1}}$
i.e. $P{{E}_{1}}=\dfrac{1}{2}K{{r}^{2}}$ …… (1)
Similarly, we use the above formula for spring ${{S}_{2}}$
i.e.$P{{E}_{2}}=\dfrac{1}{2}2K\text{ }{{x}^{2}}$ …… (2)
Now, dividing equation (2) by equation (1)
We get $\dfrac{P{{E}_{2}}}{P{{E}_{1}}}=\dfrac{1}{2}K{{x}^{2}}\times \dfrac{2}{\left( 2K \right){{x}^{2}}}$
Now, cancelling all the common factors in the above equation we get
$\dfrac{P{{E}_{2}}}{P{{E}_{1}}}=\dfrac{1}{2}$
Or for simplicity we can write this as also
$\dfrac{P{{E}_{2}}}{P{{E}_{1}}}=\dfrac{1}{2}$
Therefore, the ratio of the two potential angles is $2:1$
Note Above discussion of Potential Energy that is stored in the spring can be found out using $\dfrac{1}{2}k{{x}^{2}}$formula in which$k=\text{Spring Constant}$.
In this case, we reciprocate this energy with respect to the other.
Here, two springs are converted in series
Therefore, using $P.E=\dfrac{1}{2}{{K}_{2}}$
Complete Step by Step Solution
$2:1$
For spring ${{S}_{1}}\text{ the spring constant is }K$
For spring${{S}_{2}}$ the spring constant is $2K$
Now, applying the potential energy formula for spring ${{S}_{1}}$
i.e. $P{{E}_{1}}=\dfrac{1}{2}K{{r}^{2}}$ …… (1)
Similarly, we use the above formula for spring ${{S}_{2}}$
i.e.$P{{E}_{2}}=\dfrac{1}{2}2K\text{ }{{x}^{2}}$ …… (2)
Now, dividing equation (2) by equation (1)
We get $\dfrac{P{{E}_{2}}}{P{{E}_{1}}}=\dfrac{1}{2}K{{x}^{2}}\times \dfrac{2}{\left( 2K \right){{x}^{2}}}$
Now, cancelling all the common factors in the above equation we get
$\dfrac{P{{E}_{2}}}{P{{E}_{1}}}=\dfrac{1}{2}$
Or for simplicity we can write this as also
$\dfrac{P{{E}_{2}}}{P{{E}_{1}}}=\dfrac{1}{2}$
Therefore, the ratio of the two potential angles is $2:1$
Note Above discussion of Potential Energy that is stored in the spring can be found out using $\dfrac{1}{2}k{{x}^{2}}$formula in which$k=\text{Spring Constant}$.
In this case, we reciprocate this energy with respect to the other.
Recently Updated Pages
How to find Oxidation Number - Important Concepts for JEE

How Electromagnetic Waves are Formed - Important Concepts for JEE

Electrical Resistance - Important Concepts and Tips for JEE

Average Atomic Mass - Important Concepts and Tips for JEE

Chemical Equation - Important Concepts and Tips for JEE

Concept of CP and CV of Gas - Important Concepts and Tips for JEE

Trending doubts
JEE Main 2025 Session 2: Application Form (Out), Exam Dates (Released), Eligibility, & More

JEE Main Exam Marking Scheme: Detailed Breakdown of Marks and Negative Marking

JEE Main 2025: Derivation of Equation of Trajectory in Physics

Electric Field Due to Uniformly Charged Ring for JEE Main 2025 - Formula and Derivation

Degree of Dissociation and Its Formula With Solved Example for JEE

Physics Average Value and RMS Value JEE Main 2025

Other Pages
Units and Measurements Class 11 Notes: CBSE Physics Chapter 1

JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

NCERT Solutions for Class 11 Physics Chapter 1 Units and Measurements

JEE Advanced 2025: Dates, Registration, Syllabus, Eligibility Criteria and More

Motion in a Straight Line Class 11 Notes: CBSE Physics Chapter 2

JEE Advanced Weightage 2025 Chapter-Wise for Physics, Maths and Chemistry




