Question

Two squares have a total size of 20 square centimeters. One square's side is twice as long as the other square's side. How do you calculate the lengths of each square's sides?

Answer 1

Hint:We will assume the length of side of both squares. We will use the formula and find the area of both squares. Using the relation between the sides we will put the values of the sides. We will put the sum of the values of the area of both square equals to 20.

Complete step by step answer:
We will assume the side of smaller square equals to x cm
We have given one square's side is twice as long as the other square's side
So, the length of bigger square is 2x cm

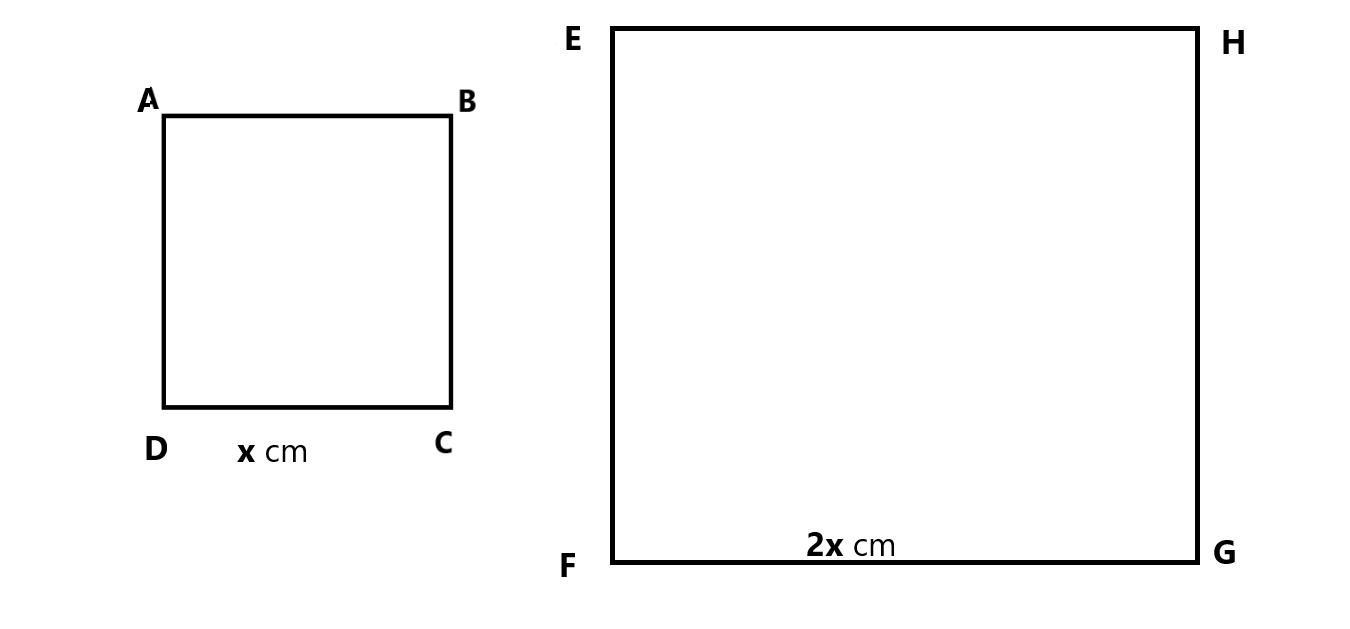
We have given the sum of area of both square is 20
Now, we will find the area of both square
We know that the formula of area of square \[ = {\left( {side} \right)^2}\]
So, the area of square having side x cm
\[ \Rightarrow A = x \times x = {x^2}\]
Area of square having side 2x cm
\[ \Rightarrow A = 2x \times 2x = 4{x^2}\]
We have given the sum of area of both square is 20
$ \Rightarrow {x^2} + 4{x^2} = 20$
$ \Rightarrow 5{x^2} = 20$
We have divided both side by 5
$ \Rightarrow {x^2} = 4$
We have taken root to both side
$ \Rightarrow x = \pm 2$
We know the side cannot be negative so, the side is 2 cm
And the length of bigger square is 4 cm
Hence, the length of side of 2 square is 2 cm and 4 cm ${x^2} = 4$

Note: We used only positive square roots to solve the equation ${x^2} = 4$ in the answer because ‘x' is the length of a side, and the length of a side of a square cannot be negative. The same thing is applied for the area of the square.