
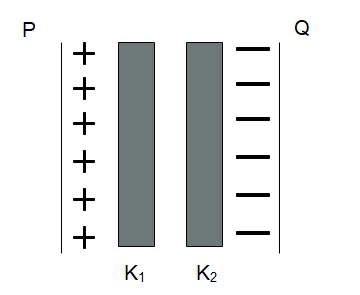
Two thin dielectric slabs of dielectric constants
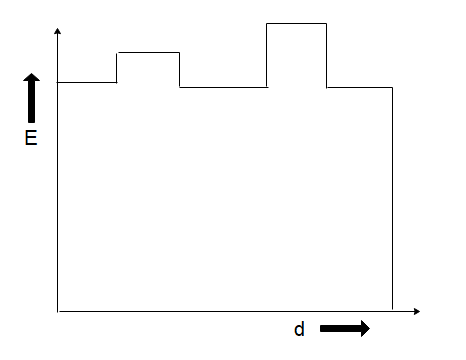
A)
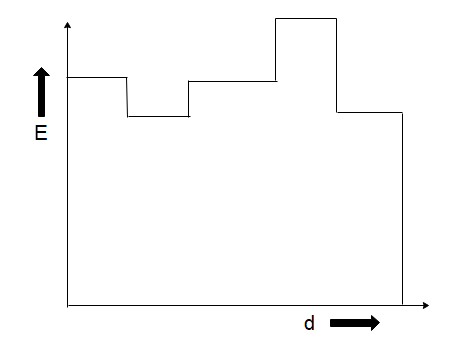
B)
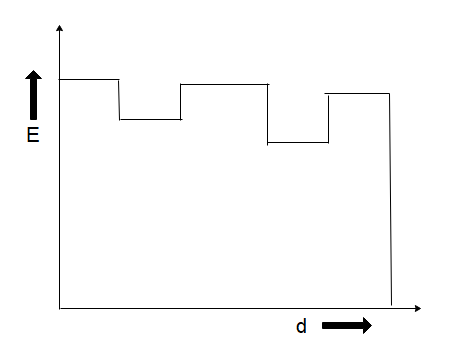
C)
D)





Answer
450.6k+ views
1 likes
Hint: When a dielectric is present between the plates of a capacitor, it will modify the electric field that exists between the two plates of the capacitor. Charges will be induced in the dielectric such that it will produce an electric field opposing the original electric field.
Formula used:
In this solution we will be using the following formula:
Dielectric field in presence of a dielectric:
Complete answer:
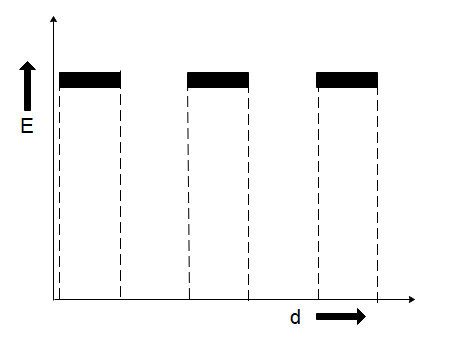
In the absence of a dielectric field, a uniform electric field is present between the capacitor plates. However, when a dielectric is present, as mentioned in the hint, an electric field will be induced in it such that it will oppose the external electric field. This is due to the polarization of charges inside the dielectric material. Hence the electric field in the region of the dielectrics will be smaller than the external electric field.
Moreover, the stronger the dielectric, the stronger the electric field will be induced, and hence even a lower electric field will exist in that region due to higher opposition of the external electric field.
Since
Hence the correct choice is option (C).
Note:
The electric field induced in a dielectric will always be lower than the external electric field. If a very strong electric field is applied, the dielectric breakdown might take place and then the dielectric will no longer be able to oppose the external electric field.
Formula used:
In this solution we will be using the following formula:
Dielectric field in presence of a dielectric:
Complete answer:
In the absence of a dielectric field, a uniform electric field is present between the capacitor plates. However, when a dielectric is present, as mentioned in the hint, an electric field will be induced in it such that it will oppose the external electric field. This is due to the polarization of charges inside the dielectric material. Hence the electric field in the region of the dielectrics will be smaller than the external electric field.
Moreover, the stronger the dielectric, the stronger the electric field will be induced, and hence even a lower electric field will exist in that region due to higher opposition of the external electric field.
Since
Hence the correct choice is option (C).
Note:
The electric field induced in a dielectric will always be lower than the external electric field. If a very strong electric field is applied, the dielectric breakdown might take place and then the dielectric will no longer be able to oppose the external electric field.
Latest Vedantu courses for you
Grade 9 | CBSE | SCHOOL | English
Vedantu 9 CBSE Pro Course - (2025-26)
School Full course for CBSE students
₹35,000 per year
Recently Updated Pages
Express the following as a fraction and simplify a class 7 maths CBSE

The length and width of a rectangle are in ratio of class 7 maths CBSE

The ratio of the income to the expenditure of a family class 7 maths CBSE

How do you write 025 million in scientific notatio class 7 maths CBSE

How do you convert 295 meters per second to kilometers class 7 maths CBSE

Write the following in Roman numerals 25819 class 7 maths CBSE

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

What are Quantum numbers Explain the quantum number class 11 chemistry CBSE

Write the differences between monocot plants and dicot class 11 biology CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light

In northern hemisphere 21st March is called as A Vernal class 11 social science CBSE




