
When two thin lenses are kept in contact, prove that their combined or effective focal length F is given by $\dfrac{1}{F}=\dfrac{1}{{{f}_{1}}}+\dfrac{1}{{{f}_{2}}}$ where the terms have their usual meaning.
Answer
567.9k+ views
Hint: Let two thin lenses ${{L}_{1}}\text{ and }{{L}_{2}}$ of focal lengths ${{f}_{1}}\text{ and }{{f}_{2}}$ be placed in contact so as to have a common principal axis. It is required to find the effective focal length of this combination. Let O be a point object on the principal axis.
Complete step by step answer:
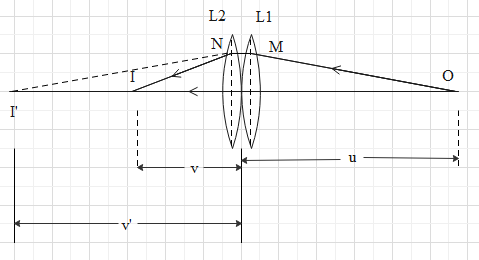
In the above figure two lenses are kept in contact and image is traced. We will solve accordingly to find the new focal length obtained by the two.
We know that the refraction through the two lenses are considered separately and the results are combined. While dealing with the individual lenses, the distances are to be measured from the respective optic centres. Since the lenses are thin, these distances can also be measured from the centre of the lens system (point of contact in the case of two lenses).
Let u be the distance of O from the centre of the lens system. Assuming that the lens ${{L}_{1}}$alone produces the refraction.
Let the image be formed at I at a distance v.
Writing the lens equation in this case. We get
$\Rightarrow \dfrac{1}{u}+\dfrac{1}{v'}=\dfrac{1}{{{f}_{1}}}$
The image I’ due to the first lens acts on the virtual object for the second lens. Let the final image be formed at I, at a distance v from the centre of the lens system. Writing the lens equation in this case, we get
\[\Rightarrow \dfrac{1}{-v'}+\dfrac{1}{v}=\dfrac{1}{{{f}_{2}}}\]
Adding equations in both the cases we get
\[\begin{align}
& \dfrac{1}{u}+\dfrac{1}{v'}-\dfrac{1}{v'}+\dfrac{1}{v}=\dfrac{1}{{{f}_{1}}}+\dfrac{1}{{{f}_{2}}} \\
& \dfrac{1}{u}+\dfrac{1}{v}=\dfrac{1}{{{f}_{1}}}+\dfrac{1}{{{f}_{2}}}.............1 \\
\end{align}\]
Let the two lenses be replaced by a single lens which can produce the same effect as the two lenses put together produce, i.e., for an object O placed at a distance u from it, the image I must be formed at a distance v. such a lens is called an equivalent lens and its focal length is called the equivalent focal length.
Writing the lens equation in this case, we get
\[\Rightarrow \dfrac{1}{u}-\dfrac{1}{v}=\dfrac{1}{f}............2\]
Comparing equations (1) and (2) we get
$\Rightarrow \dfrac{1}{F}=\dfrac{1}{{{f}_{1}}}+\dfrac{1}{{{f}_{2}}}$
The below given figure shows that combination of two lenses will behave as a single lens having focal length equal to the sum of the reciprocals of the individual focal lengths.
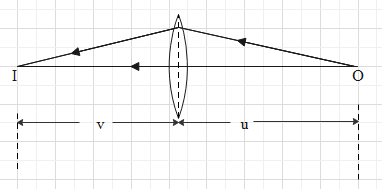
Hence, when thin lenses are combined, the reciprocal of the effective focal length will be equal to the sum of the reciprocals of the individual focal lengths.
Note:
We use a combination of lenses to increase the sharpness of the final image by minimising certain defects or aberrations in it. Minimising certain defects or aberrations in it. To erect the final image. We also use it to increase the field of view.
Complete step by step answer:

In the above figure two lenses are kept in contact and image is traced. We will solve accordingly to find the new focal length obtained by the two.
We know that the refraction through the two lenses are considered separately and the results are combined. While dealing with the individual lenses, the distances are to be measured from the respective optic centres. Since the lenses are thin, these distances can also be measured from the centre of the lens system (point of contact in the case of two lenses).
Let u be the distance of O from the centre of the lens system. Assuming that the lens ${{L}_{1}}$alone produces the refraction.
Let the image be formed at I at a distance v.
Writing the lens equation in this case. We get
$\Rightarrow \dfrac{1}{u}+\dfrac{1}{v'}=\dfrac{1}{{{f}_{1}}}$
The image I’ due to the first lens acts on the virtual object for the second lens. Let the final image be formed at I, at a distance v from the centre of the lens system. Writing the lens equation in this case, we get
\[\Rightarrow \dfrac{1}{-v'}+\dfrac{1}{v}=\dfrac{1}{{{f}_{2}}}\]
Adding equations in both the cases we get
\[\begin{align}
& \dfrac{1}{u}+\dfrac{1}{v'}-\dfrac{1}{v'}+\dfrac{1}{v}=\dfrac{1}{{{f}_{1}}}+\dfrac{1}{{{f}_{2}}} \\
& \dfrac{1}{u}+\dfrac{1}{v}=\dfrac{1}{{{f}_{1}}}+\dfrac{1}{{{f}_{2}}}.............1 \\
\end{align}\]
Let the two lenses be replaced by a single lens which can produce the same effect as the two lenses put together produce, i.e., for an object O placed at a distance u from it, the image I must be formed at a distance v. such a lens is called an equivalent lens and its focal length is called the equivalent focal length.
Writing the lens equation in this case, we get
\[\Rightarrow \dfrac{1}{u}-\dfrac{1}{v}=\dfrac{1}{f}............2\]
Comparing equations (1) and (2) we get
$\Rightarrow \dfrac{1}{F}=\dfrac{1}{{{f}_{1}}}+\dfrac{1}{{{f}_{2}}}$
The below given figure shows that combination of two lenses will behave as a single lens having focal length equal to the sum of the reciprocals of the individual focal lengths.

Hence, when thin lenses are combined, the reciprocal of the effective focal length will be equal to the sum of the reciprocals of the individual focal lengths.
Note:
We use a combination of lenses to increase the sharpness of the final image by minimising certain defects or aberrations in it. Minimising certain defects or aberrations in it. To erect the final image. We also use it to increase the field of view.
Recently Updated Pages
Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Trending doubts
What are the major means of transport Explain each class 12 social science CBSE

Which are the Top 10 Largest Countries of the World?

Draw a labelled sketch of the human eye class 12 physics CBSE

How much time does it take to bleed after eating p class 12 biology CBSE

Explain sex determination in humans with line diag class 12 biology CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE




