
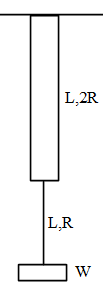
Two wires of the same material (young’s modulus Y) and same length L but radii R and 2R respectively are joined end to end and a weight W is suspended from the combination as shown in the figure. The elastic potential energy in the system in equilibrium is:
A) $\dfrac{{3{W^2}L}}{{4\pi {R^2}Y}}$.
B) $\dfrac{{3{W^2}L}}{{8\pi {R^2}Y}}$.
C) $\dfrac{{5{W^2}L}}{{8\pi {R^2}Y}}$.
D) $\dfrac{{{W^2}L}}{{\pi {R^2}Y}}$.
Answer
219.6k+ views
Hint: The potential energy is the energy which is saved inside the wire and is caused due to the elongation of the wire. The young’s modulus of a material is defined as the ratio of the stress and strain and it is constant till the proportional limit.
Formula used: The formula of the potential energy is given by,
$ \Rightarrow E = \dfrac{{{F^2}L}}{{2AY}}$
Where force is F, the original length is L, the area is A and Young’s modulus is Y.
Complete step by step solution:
It is given in the problem that the two wires of the same material (young’s modulus Y) and same length L but radii R and 2R respectively are joined end to end and a weight W is suspended from the combination and we need to find the elastic potential energy in the system in equilibrium condition.
The formula of the potential energy is given by,
$ \Rightarrow E = \dfrac{{{F^2}L}}{{2AY}}$
Where force is F, the original length is L, the area is A and Young’s modulus is Y.
The potential energy of the wire is equal to,
$ \Rightarrow E = \dfrac{{{F^2}L}}{{2AY}}$
The elongation is taking place in the two parts of the wires.
The potential energy of the system is equal to,
$ \Rightarrow E = \dfrac{{{W^2}L}}{{2{A_1}Y}} + \dfrac{{{W^2}L}}{{2{A_2}Y}}$
$ \Rightarrow E = \dfrac{{{W^2}L}}{{2\left( {\pi {R^2}} \right)Y}} + \dfrac{{{W^2}L}}{{2\pi {{\left( {2R} \right)}^2}Y}}$
$ \Rightarrow E = \dfrac{{{W^2}L}}{{2\pi {R^2}Y}} + \dfrac{{{W^2}L}}{{8\pi {R^2}Y}}$
$ \Rightarrow E = \dfrac{{2{W^2}L + {W^2}L}}{{8\pi {R^2}Y}}$
$ \Rightarrow E = \dfrac{{3{W^2}L}}{{8\pi {R^2}Y}}$.
The potential energy of the wire is equal to $E = \dfrac{{3{W^2}L}}{{8\pi {R^2}Y}}$. The correct option for this problem is option B.
Note: The students are advised to understand and remember the formula of the potential energy of the wire as it is very useful in solving these kinds of problems. The change of the length happens due to the applied force or the load due to weight.
Formula used: The formula of the potential energy is given by,
$ \Rightarrow E = \dfrac{{{F^2}L}}{{2AY}}$
Where force is F, the original length is L, the area is A and Young’s modulus is Y.
Complete step by step solution:
It is given in the problem that the two wires of the same material (young’s modulus Y) and same length L but radii R and 2R respectively are joined end to end and a weight W is suspended from the combination and we need to find the elastic potential energy in the system in equilibrium condition.
The formula of the potential energy is given by,
$ \Rightarrow E = \dfrac{{{F^2}L}}{{2AY}}$
Where force is F, the original length is L, the area is A and Young’s modulus is Y.
The potential energy of the wire is equal to,
$ \Rightarrow E = \dfrac{{{F^2}L}}{{2AY}}$
The elongation is taking place in the two parts of the wires.
The potential energy of the system is equal to,
$ \Rightarrow E = \dfrac{{{W^2}L}}{{2{A_1}Y}} + \dfrac{{{W^2}L}}{{2{A_2}Y}}$
$ \Rightarrow E = \dfrac{{{W^2}L}}{{2\left( {\pi {R^2}} \right)Y}} + \dfrac{{{W^2}L}}{{2\pi {{\left( {2R} \right)}^2}Y}}$
$ \Rightarrow E = \dfrac{{{W^2}L}}{{2\pi {R^2}Y}} + \dfrac{{{W^2}L}}{{8\pi {R^2}Y}}$
$ \Rightarrow E = \dfrac{{2{W^2}L + {W^2}L}}{{8\pi {R^2}Y}}$
$ \Rightarrow E = \dfrac{{3{W^2}L}}{{8\pi {R^2}Y}}$.
The potential energy of the wire is equal to $E = \dfrac{{3{W^2}L}}{{8\pi {R^2}Y}}$. The correct option for this problem is option B.
Note: The students are advised to understand and remember the formula of the potential energy of the wire as it is very useful in solving these kinds of problems. The change of the length happens due to the applied force or the load due to weight.
Recently Updated Pages
Chemical Equation - Important Concepts and Tips for JEE

JEE Main 2022 (July 29th Shift 1) Chemistry Question Paper with Answer Key

Conduction Explained: Definition, Examples & Science for Students

Analytical Method of Vector Addition Explained Simply

Atomic Size - Important Concepts and Tips for JEE

JEE Main 2022 (June 29th Shift 1) Maths Question Paper with Answer Key

Trending doubts
JEE Main 2026: Application Form Open, Exam Dates, Syllabus, Eligibility & Question Papers

Understanding Uniform Acceleration in Physics

Derivation of Equation of Trajectory Explained for Students

Hybridisation in Chemistry – Concept, Types & Applications

Understanding the Angle of Deviation in a Prism

Understanding Collisions: Types and Examples for Students

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Units And Measurements Class 11 Physics Chapter 1 CBSE Notes - 2025-26

NCERT Solutions For Class 11 Physics Chapter 8 Mechanical Properties Of Solids

Motion in a Straight Line Class 11 Physics Chapter 2 CBSE Notes - 2025-26

NCERT Solutions for Class 11 Physics Chapter 7 Gravitation 2025-26

Mechanical Properties of Fluids Class 11 Physics Chapter 9 CBSE Notes - 2025-26




