Question

How do you use the epsilon delta definition to find the limit of \[\left( {\dfrac{{{x^2} + x - 6}}{{x - 2}}} \right)\]as \[x\] approaches \[2\]\[?\]

Answer 1

Hint: Here we have to check that the given function is defined or not at \[x = 2\]. If it is defined, then by the definition epsilon delta finds the relationship between epsilon and delta to prove the limit of the given function as \[x\]approaches to \[2\] it exists and is unique.

Complete step by step solution:
The epsilon-delta definition of limits says that the limit of \[f(x)\]at \[x = c\]is \[L\] if for any \[\varepsilon > 0\] there exists a \[\delta > 0\] such that if the distance of \[x\] from \[c\] is less than \[\delta \], then the distance of f(x) from \[L\] is less than \[\varepsilon \].
Graphical representation of the epsilon-delta definition:

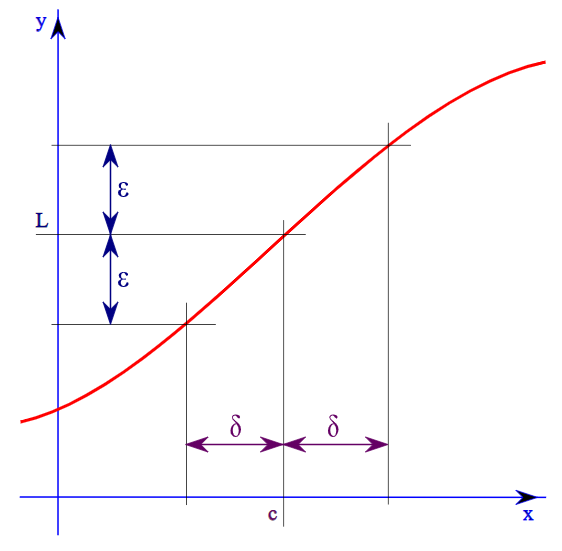
Let the given function say \[f(x) = \left( {\dfrac{{{x^2} + x - 6}}{{x - 2}}} \right)\] and \[L\] be the limit of the given function.
At \[x = 2\], the given function approaches infinity. So, rewriting the given above function, we get \[f(x) = x + 3\]. Hence at \[x = 2\],\[f(2) = 5\].
\[ \Rightarrow \] \[\mathop {\lim }\limits_{x \to 2} \left( {\dfrac{{{x^2} + x - 6}}{{x - 2}}} \right) = 5\]
We prove by the epsilon delta definition, for any \[\varepsilon > 0\] there exists a \[\delta > 0\] such that
If \[\left| {x - 2} \right| < \delta \] \[ \Rightarrow \] \[\left| {f(x) - L} \right| < \varepsilon \]
\[ \Rightarrow \left| {x + 3 - 5} \right| < \varepsilon \]
On simplification,
\[ \Rightarrow \left| {x + 2} \right| < \varepsilon \]
\[ \Rightarrow \left| {x + 2} \right| < \delta \]
From the above two equations, we can say
\[ \delta = \varepsilon \]
Hence the limit of \[\left( {\dfrac{{{x^2} + x - 6}}{{x - 2}}} \right)\]as \[x\] approaches \[2\] is \[5\].

Note:
Note that If the limit of the given function at the given point exists then the limit is unique and finite. A function is continuous if you can draw its graph without lifting the pencil. Every differentiable function is continuous but converse is not true.