Question

Use Venn diagrams to verify De’ Morgan’s law of complementation ${\left( {A \cup B} \right)^\prime } = \left( {A' \cap B'} \right)$

Answer 1

Hint: In this particular question use the concept that if set A has particular elements and set B has also some particular elements different from set A but some elements are same then in the set $\left( {A \cup B} \right)$ has all the elements containing set A and set B, common terms only written one time, in the set A’ there is no element which is in set A, so A’ is also called as a null set, so use these concepts to reach the solution of the question.

Complete step-by-step solution:
We have to verify using Venn diagrams De’ Morgan’s law of complementation i.e. ${\left( {A \cup B} \right)^\prime } = \left( {A' \cap B'} \right)$
I.e. complement of the union of the two sets is equal to the intersection of the complements of the respective set.
Now consider the LHS of the above equation we have,
$ \Rightarrow {\left( {A \cup B} \right)^\prime }$
Now as we know that if set A has particular elements and set B has also some particular elements different from set A but some elements are the same then in the set $\left( {A \cup B} \right)$ (i.e. A union B) has all the elements containing set A and set B, common terms only written one time, as shown in the Venn diagrams below.
Now ${\left( {A \cup B} \right)^\prime }$ is nothing but the complement of $\left( {A \cup B} \right)$ as shown in the Venn diagram below.

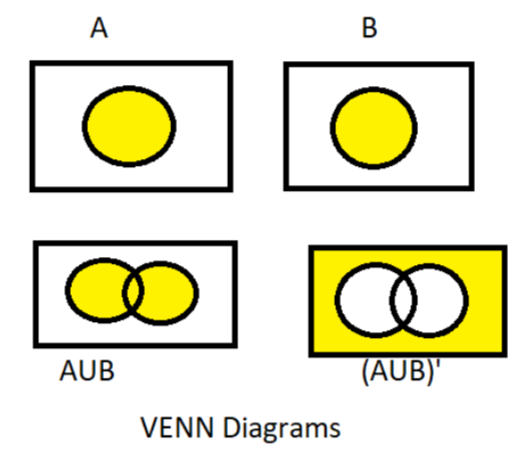
So ${\left( {A \cup B} \right)^\prime }$ is a null set i.e. a set which does not contain any elements.
Now consider the RHS of the above equation we have,
$ \Rightarrow \left( {A' \cap B'} \right)$
Now as we know that in set A’ there is no element of A as shown in the Venn diagram below similarly for the B’ or we can say that A’ and B’ is the complement of A and B respectively.
So A’ and B’ have no elements of A and B respectively.
So, $\left( {A' \cap B'} \right)$ has also no elements of A and B as shown below in the Venn diagrams.

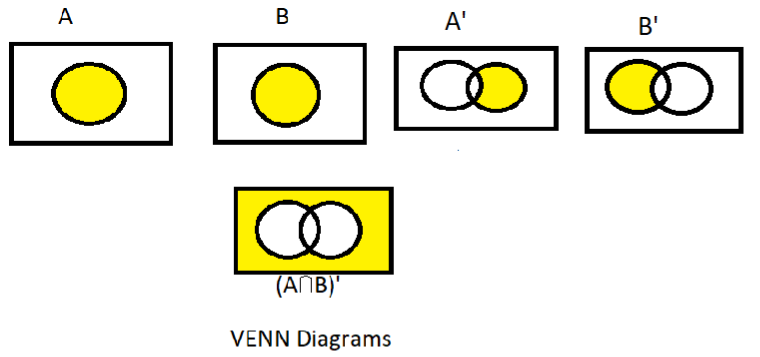
So from the first and second Venn diagram, we can say that
LHS = RHS
Hence proved.

Note: Whenever we face such types of questions the key concept we have to remember is that always recall the following symbols which is given as,
$ \cup $ = union
$ \cap = $Intersection
$A'$ = complement of A
And the other De’ Morgan’s law is given as ${\left( {A \cap B} \right)^\prime } = \left( {A' \cup B'} \right)$