
Using Gauss’s law obtain the expression for the electric field due to the uniformly charged thin spherical shell of radius
Answer
488.1k+ views
Hint A uniformly charged sphere is spherically symmetric i.e. all points around the sphere are identical. Therefore, choose a spherical Gaussian surface whose radius is equal to the distance
Formula used:
Complete step by step answer
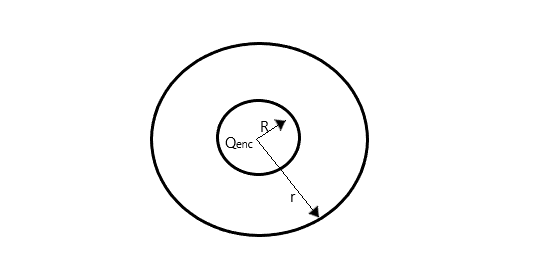
Gauss law allows us to easily find the electric field of a charge distribution by taking advantage of a possible symmetry in its arrangement. From integral form of Gauss law, we have
For a uniform spherical charge, the equation becomes
Then,
Rearranging for
The electric field for a uniformly charged thin spherical shell at radius
Hence, the graph of electric field with distance is as shown below.
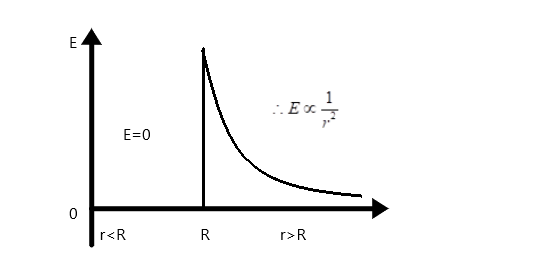
Note
For
For
Also,
For
Formula used:
Complete step by step answer

Gauss law allows us to easily find the electric field of a charge distribution by taking advantage of a possible symmetry in its arrangement. From integral form of Gauss law, we have
For a uniform spherical charge, the equation becomes
Then,
Rearranging for
The electric field for a uniformly charged thin spherical shell at radius
Hence, the graph of electric field with distance is as shown below.

Note
For
For
Also,
For
Recently Updated Pages
Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Class 12 Question and Answer - Your Ultimate Solutions Guide

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Trending doubts
Draw a labelled sketch of the human eye class 12 physics CBSE

a Tabulate the differences in the characteristics of class 12 chemistry CBSE

Which one of the following is a true fish A Jellyfish class 12 biology CBSE

Why is the cell called the structural and functional class 12 biology CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Write the difference between solid liquid and gas class 12 chemistry CBSE




