Question

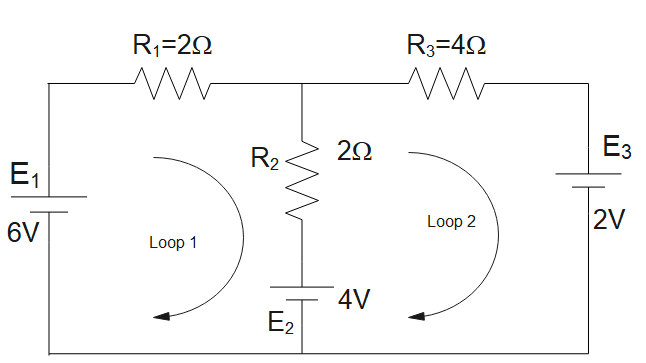
Using KVL and KCL find the branch currents in the given circuit

Answer 1

Hint: There are basically two Kirchhoff’s Laws, these laws play a very crucial role in electronics. Kirchhoff's first law states that the algebraic sum of current flowing through a junction is always zero, this law is also known as Kirchhoff’s Current Law as this law deals with the current. The other form of this law, we can say that at any node the incoming current is always equal to outgoing current for a particular instant of time.

Complete step by step answer:
In this question, we have been asked to find the current in each of the branch. We have already been given two loops in the question with their direction, so we will move according to them
In loop 1, using KVL we get
$2{{I}_{1}}+2({{I}_{1}}-{{I}_{2}})=4-6$
$4{{I}_{1}}-2{{I}_{2}}=-2$ ………… (1)
In loop 2, using KVL we get
$4{{I}_{2}}+2({{I}_{2}}-{{I}_{1}})=-2-4$
$6{{I}_{2}}-2{{I}_{1}}=-6$ …………….. (2)
On solving both equation (1) and equation (2), we get
${{I}_{1}}=-1.2A$
${{I}_{2}}=-1.4A$
Here the negative sign indicates that the direction that we have chosen as positive is wrong and current moves in opposite direction as of what we have selected
Hence, Instead of anti-clockwise direction the current moves in clockwise direction.
Hence, the correct answer to our question is
${{I}_{1}}=1.2A$
${{I}_{2}}=1.4A$

Note: Sometimes we get a negative value of current that simply denotes that the actual direction of movement of current is opposite of what we have selected in our loop. Negative sign does not indicate that the current is negative, it just denotes the direction, if we start solving the question with exactly the opposite direction as that of what we have solved before, we will get the value of current as positive.