Question

Using the method of integration, find the area of the region bounded by the following lines $5x-2y-10=0, x+y-9=0\text{ and }2x-5y-4=0$

Answer 1

Hint: We have equation of three lines as:
$\begin{align}
  & 5x-2y-10=0......(1) \\
 & x+y-9=0......(2) \\
 & 2x-5y-4=0......(3)
\end{align}$
Find the points of intersection of each line by getting values of x and y for each pair of lines. We get three points of intersection that form a triangle. Hence, the area of the region bounded by the given lines in the area of the triangle.
Area using integration method for function is given as: $A=\int_{a}^{b}{f(x)dx}$, where a and b are lower and upper limit of the function respectively. So, to find the area using the integration method, we need to identify the curves either in terms of y or x and put the extreme values, i.e. points of intersection, and solve the definite integral to calculate the area bounded by the lines.

Complete step-by-step solution:
Since we have the following equations of line:
$\begin{align}
  & 5x-2y-10=0......(1) \\
 & x+y-9=0......(2) \\
 & 2x-5y-4=0......(3)
\end{align}$
We can write equation (1), (2) and (3) as equation (4), (5) and (6) respectively:
$\begin{align}
  & y=\dfrac{5}{2}\left( x-2 \right).......(4) \\
 & y=-\left( x-9 \right)......(5) \\
 & y=\dfrac{2}{5}\left( x-2 \right).......(6) \\
\end{align}$
Now, we need to find points of intersection of each line.
For line (1) and (2), equate the equation (4) and (5), we get:
$\begin{align}
  & \Rightarrow \dfrac{5}{2}\left( x-2 \right)=-\left( x-9 \right) \\
 & \Rightarrow 5x-10=-2x+18 \\
 & \Rightarrow x=4 \\
\end{align}$
Put the value of x in equation (4), we get:
$\begin{align}
  & \Rightarrow y=\dfrac{5}{2}\left( 4-2 \right) \\
 & \Rightarrow y=5 \\
\end{align}$
Hence, point of intersection of line (1) and (2) is $\left( 4,5 \right)$
Similarly, for line (2) and (3), equate the equation (5) and (6), we get:
$\begin{align}
  & \Rightarrow -\left( x-9 \right)=\dfrac{2}{5}\left( x-2 \right) \\
 & \Rightarrow -5x+45=2x-4 \\
 & \Rightarrow x=7 \\
\end{align}$
Put the value of x in equation (5), we get:
$\begin{align}
  & \Rightarrow y=-\left( 7-9 \right) \\
 & \Rightarrow y=2 \\
\end{align}$
Hence, point of intersection of line (2) and (3) is $\left( 7,2 \right)$
Also, for line (1) and (3), equate the equation (4) and (6), we get:
\[\begin{align}
  & \Rightarrow \dfrac{5}{2}\left( x-2 \right)=\dfrac{2}{5}\left( x-2 \right) \\
 & \Rightarrow 25x-50=4x-8 \\
 & \Rightarrow x=2 \\
\end{align}\]
Put the value of x in equation (6), we get:
$\begin{align}
  & \Rightarrow y=\dfrac{2}{5}\left( 2-2 \right) \\
 & \Rightarrow y=0 \\
\end{align}$
Hence, point of intersection of line (1) and (3) is $\left( 2,0 \right)$
Hence, we have triangle ABC formed with the intersection points of the three lines. It is shown with the help of a diagram below:

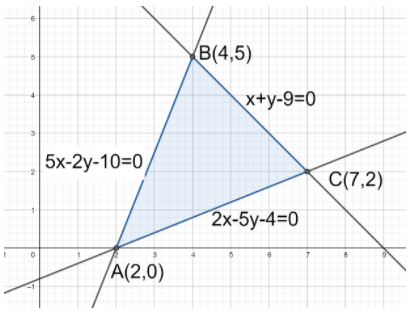
Now, we need to find the area of triangle ABC using the integration method.
The area using integration method for function is given as: $A=\int_{a}^{b}{f(x)dx}$, where a and b are lower and upper limit of the function respectively.
So, we need to identify the curves and the endpoints for the integration.
Let us consider the figure given below:

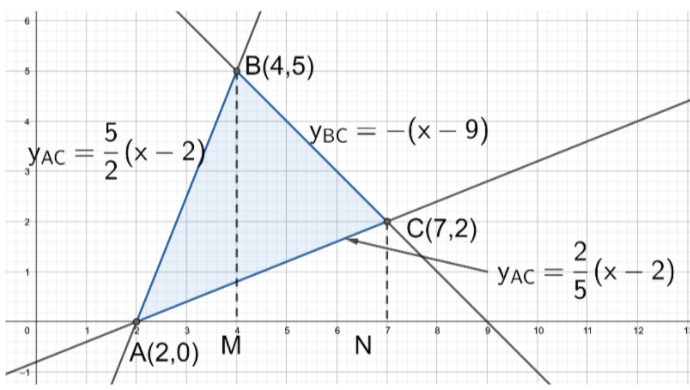
In this figure, $\Delta ABC$ is the region bounded by the given lines. Draw a perpendicular BM from B and CN from C to the x-axis.
Since, we need to find the area of $\Delta ABC$, from the figure we can say that
Area of $\Delta ABC$ = Area of $\Delta ABM$ + Area of Trapezium BMNC - Area of $\Delta ACN$
In $\Delta ABM$, we have an upper curve as $y=\dfrac{5}{2}\left( x-2 \right)$ and the lower curve is x-axis, i.e. y=0. So, the upper limit is x=4 and the lower limit is x=2.
So, \[Area\text{ }of\Delta ABM=\int\limits_{2}^{4}{\dfrac{5}{2}\left( x-2 \right)dx}......(7)\]
Similarly, in Trapezium BMNC, we have the upper curve as $y=-\left( x-9 \right)$ and the lower curve is x-axis, i.e. y=0. So, the upper limit is x=7 and the lower limit is x=4.
So, \[Area\text{ }of~Trapezium\text{ }BMNC=\int\limits_{5}^{7}{-\left( x-9 \right)dx......(8)}\]
Also, In $\Delta ACN$, we have curve upper curve as $y=\dfrac{2}{5}\left( x-2 \right)$ and lower curve is x-axis, i.e. y=0. So, the upper limit is x=7 and the lower limit is x=2.
So, \[Area\text{ }of\Delta ACN=\int\limits_{2}^{7}{\dfrac{2}{5}\left( x-2 \right)dx}......(9)\]
So, we can write that:
Area of $\Delta ABC$\[=\int\limits_{2}^{4}{\dfrac{5}{2}\left( x-2 \right)dx}+\int\limits_{4}^{7}{-\left( x-9 \right)dx}-\int\limits_{2}^{7}{\dfrac{2}{5}\left( x-2 \right)dx}......(10)\]
Now, solve the integration, we get:
Area of $\Delta ABC$
\[\begin{align}
& =\dfrac{5}{2}\left( \dfrac{{{x}^{2}}}{2}-2x \right)_{2}^{4}-\left( \dfrac{{{x}^{2}}}{2}-9x \right)_{4}^{7}-\dfrac{2}{5}\left( \dfrac{{{x}^{2}}}{2}-2x \right)_{2}^{7} \\
& =\dfrac{5}{2}\left( 8-8-2+4 \right)-\left( \dfrac{49}{2}-63-\dfrac{16}{2}+36 \right)-\dfrac{2}{5}\left( \dfrac{49}{2}-14-\dfrac{4}{2}+4 \right) \\
 & =\dfrac{5}{2}\left( 2 \right)-\left( \dfrac{33}{2}-33 \right)-\dfrac{2}{5}\left( \dfrac{45}{2}-10 \right) \\
 & =5+\dfrac{33}{2}-5 \\
 & =\dfrac{33}{2}=16.5 \\
\end{align}\]
Hence, area bounded by three lines is 10.5 square units.

Note: Be careful while identifying the curve as well as the upper and lower limit for integral function. If the function is in terms of y, then the upper and lower limits should be y-coordinates of points of intersection of lines. If the function is in terms of x, then the upper and lower limit should be x-coordinates of points of intersection of lines as discussed in the solution.