
When the value of R in the Balanced Wheatstone bridge shown in figure is increased from 5W to 7W, the value of S has to be increased by 3W in order to maintain the balance. What is the initial value of S ?
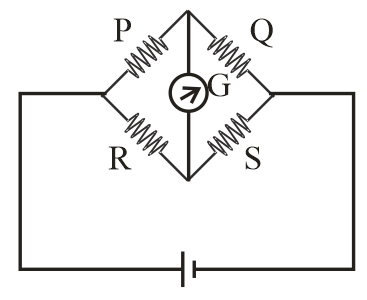
(A) 1.5W
(B) 3W
(C) 5W
(D) 7.5W

Answer
503.7k+ views
Hint:In order to solve this question,we use the balancing condition of the Wheatstone bridge which state that if
Complete Step by Step Answer:Wheatstone bridge is an arrangement of 4 resistance and galvanometer with one battery as shown in diagram.
In the balancing condition of Wheatstone bridge, the current flowing in galvanometer is zero and the relation between resistances P, Q, R & S is given as
Given that initial value of
So,
Also given that final value of
Final value of S is
So,
From equation 2 & 3
So, option D is correct answer
Note: If the current flowing in galvanometer is O, then Wheatstone is balanced & relation between P, Q, R & S is given as
If the current flowing in galvanometer is not zero then Wheatstone bridge is not balanced &
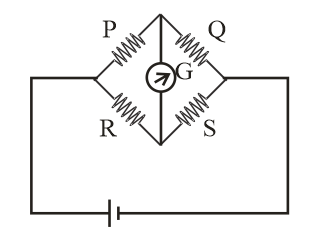
Complete Step by Step Answer:Wheatstone bridge is an arrangement of 4 resistance and galvanometer with one battery as shown in diagram.

In the balancing condition of Wheatstone bridge, the current flowing in galvanometer is zero and the relation between resistances P, Q, R & S is given as
Given that initial value of
So,
Also given that final value of
Final value of S is
So,
From equation 2 & 3
So, option D is correct answer
Note: If the current flowing in galvanometer is O, then Wheatstone is balanced & relation between P, Q, R & S is given as
If the current flowing in galvanometer is not zero then Wheatstone bridge is not balanced &
Recently Updated Pages
Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Class 12 Question and Answer - Your Ultimate Solutions Guide

Master Class 11 Economics: Engaging Questions & Answers for Success

Trending doubts
Draw a labelled sketch of the human eye class 12 physics CBSE

a Tabulate the differences in the characteristics of class 12 chemistry CBSE

Which one of the following is a true fish A Jellyfish class 12 biology CBSE

Why is the cell called the structural and functional class 12 biology CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Write the difference between solid liquid and gas class 12 chemistry CBSE




