
What is the value of unknown resistance R, in figure, if the voltage drop across
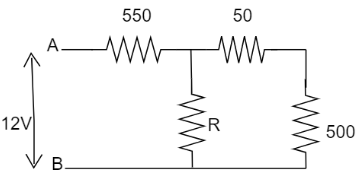

Answer
407.4k+ views
Hint:The voltage drop across the resistor connected in parallel combination is equal. The current through
Complete step by step answer:
Let us assume current (i) flows through the
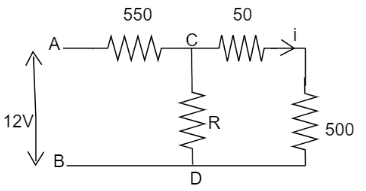
For
Now the voltage across CD branch will be calculated as:
Also by using voltage divider rule for CD branch we can write as,
Parallel combination of R and
Thus on substituting the parallel combination we get the result as,
On substituting
Rearranging the terms we get the value of R as:
Hence the value of R is
Note:Name all the nodes and branches for better understanding and representation of the problem. Apply voltage divider rule properly. We can also find the value of R by applying Kirchhoff’s voltage law in each branch respectively. The answer would be the same in both cases. Calculate the value of resistance R up to two decimal places only. Parallel combination of resistances is the ratio of product of all resistances and the sum of all resistances. In series combination, the value of current is the same through the same branch.
Complete step by step answer:
Let us assume current (i) flows through the

For
Now the voltage across CD branch will be calculated as:
Also by using voltage divider rule for CD branch we can write as,
Parallel combination of R and
Thus on substituting the parallel combination we get the result as,
On substituting
Rearranging the terms we get the value of R as:
Hence the value of R is
Note:Name all the nodes and branches for better understanding and representation of the problem. Apply voltage divider rule properly. We can also find the value of R by applying Kirchhoff’s voltage law in each branch respectively. The answer would be the same in both cases. Calculate the value of resistance R up to two decimal places only. Parallel combination of resistances is the ratio of product of all resistances and the sum of all resistances. In series combination, the value of current is the same through the same branch.
Recently Updated Pages
Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Class 12 Question and Answer - Your Ultimate Solutions Guide

Master Class 11 Economics: Engaging Questions & Answers for Success

Trending doubts
Draw a labelled sketch of the human eye class 12 physics CBSE

a Tabulate the differences in the characteristics of class 12 chemistry CBSE

Which one of the following is a true fish A Jellyfish class 12 biology CBSE

Why is the cell called the structural and functional class 12 biology CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Write the difference between solid liquid and gas class 12 chemistry CBSE




