Question

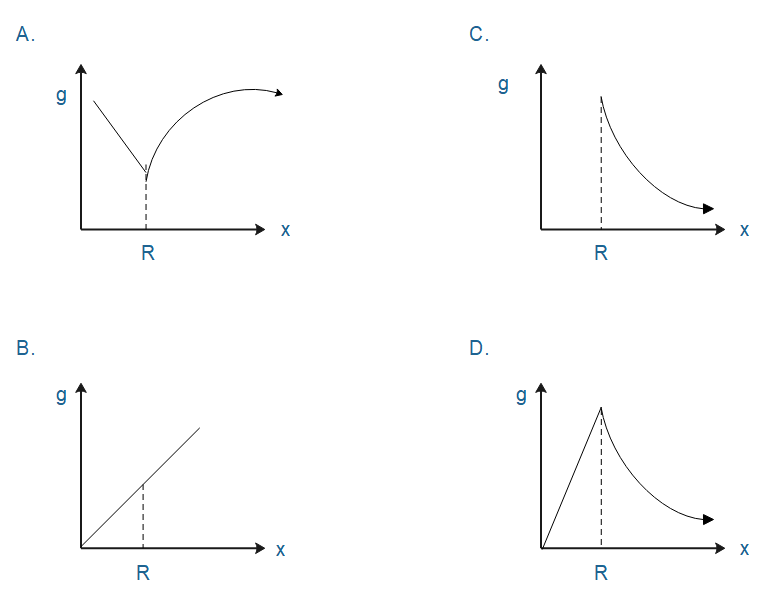
Variation of acceleration due to gravity \[\left( g \right)\] with distance $x$ from the centre of the earth is best represented by: $R\to \text{Radius of the earth}$

Answer 1

Hint: The value of $g$ is maximum at the surface of the earth and it goes on decreasing with increase in depth below the earth’s surface and with an increase in the height above the earth’s surface. The variation of acceleration due to gravity according to the depth a height from the earth surface can be expressed with the help of graph. Use \[{{g}_{h}}=\dfrac{g{{R}^{2}}}{{{(R+h)}^{2}}}\] the equation to get an idea of the graph for height and use \[{{g}_{d}}=g\left[ 1-\dfrac{d}{R} \right]\] the equation to get an idea of graph for depth.

Complete step-by-step answer:
$R$ on the x-axis represents the surface of the earth. The left portion of the graph represents acceleration due to gravity with depth. While the right portion of the graph represents acceleration due to gravity with height.
The earth exerts a gravitational force on objects near it. According to Newton’s second law of motion, a force acting on a body results in its acceleration. Thus, the gravitational force due to the earth on a body results in its acceleration. This is called acceleration due to gravity and is denoted by ‘g’. Acceleration is a vector. As the gravitational force on any object due to the earth is directed towards the centre of the earth, the direction of the acceleration due to gravity is also directed towards the centre of the earth i.e. vertically downwards.
The law of gravitation is given by,
$\begin{align}
  & F=\dfrac{GMm}{{{r}^{2}}}-----(1) \\
 & F=mg----(2) \\
 & \text{If object on the surface of earth, }g=\dfrac{GM}{{{R}^{2}}}--(3) \\
\end{align}$
As we go above the earth’s surface, the value of r in equation (1) increases and the value of g decreases. However, the decrease is rather small for heights which are small in comparison to the earth’s radius. For example, remember that the radius of the earth is 6400 km. If an aeroplane is flying at a height 10 km above the surface of the earth, its distance from the earth’s surface changes from 6400 km to 6410 km and the change in the value of g due to it is negligible. On the other hand, when we consider an artificial satellite orbiting the earth, we have to take into account the change in the value of g due to the large change in the distance of the satellite from the centre of the earth.
Equation of acceleration due to height is given by
\[{{g}_{h}}=\dfrac{g{{R}^{2}}}{{{(R+h)}^{2}}}\]
From the above equation, it is clear that acceleration due to gravity goes on decreases as the altitude of the body from the earth’s surface increases.
The value of g also changes if we go inside the earth. The value of r in equation (1) decreases and one would think that the value of g should increase as per the formula. However, the part of the earth which contributes towards the gravitational force felt by the object also decreases. Which means that the value of M to be used in equation (1) also decreases. As a combined result of a change in r and M, the value of g decreases as we go deep inside the earth.
Equation of acceleration due to depth is given by
\[{{g}_{d}}=g\left[ 1-\dfrac{d}{R} \right]\]
From above it is clear that acceleration due to gravity decreases with depth.

Note: Acceleration due to gravity depends only on the mass M and radius R of the earth and so the acceleration due to gravity at a given point on the earth is the same for all objects. It does not depend on the properties of the object. If the body of mass is taken to the centre of the earth, its weight will be equal to zero but the mass of the body will not be zero.