
Water flows through a tube as shown in the figure.
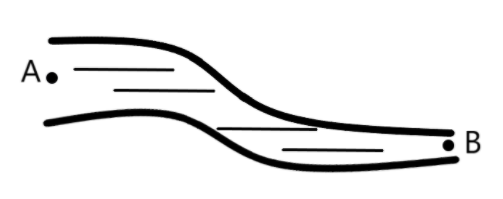
The area of cross-section at $A$ and $B$ are $1c{{m}^{3}}$ and $0.5c{{m}^{3}}$ respectively. The height difference between $A$ and $B$ is $5cm$. If the speed of water at $A$ is $10cm{{s}^{-1}}$, find
a) the speed of water at $B$
b) the difference in pressure at $A$ and $B$

Answer
483.6k+ views
Hint: Continuity equation for the flow of water suggests that the product of the speed of water and area of the cross-section at $A$ is equal to the product of the speed of water and area of the cross-section at $B$. Bernoulli’s theorem for water flow suggests that pressure difference between $A$ and $B$ is dependent on the difference in speeds of water at $A$ and $B$, the height difference between $A$ and $B$, the density of water, and acceleration due to gravity. From both these equations, the speed of the water at $B$ as well as the pressure difference between $A$ and $B$ can easily be found out.
Formula used:
$\begin{align}
& 1){{A}_{A}}{{V}_{A}}={{A}_{B}}{{V}_{B}} \\
& 2){{P}_{A}}+\dfrac{1}{2}\rho {{V}_{A}}^{2}+\rho g{{h}_{A}}={{P}_{B}}+\dfrac{1}{2}\rho {{V}_{B}}^{2}+\rho g{{h}_{B}} \\
\end{align}$
Complete step-by-step solution
We are provided with the case of water flow in a tube, as shown in the following figure.
The area of cross-section at $A$ and $B$ are $1c{{m}^{3}}$ and $0.5c{{m}^{3}}$ respectively and the height difference between $A$ and $B$ is $5cm$. If the speed of the water at $A$ is $10cm{{s}^{-1}}$, we are required to find the speed of the water at $B$ and the difference in pressure at $A$ and $B$.
From the continuity equation of water flow, we know that the product of the speed of water and area of the cross-section at $A$ is equal to the product of the speed of water and area of the cross-section at $B$. Mathematically, the equation of continuity is given by
${{A}_{A}}{{V}_{A}}={{A}_{B}}{{V}_{B}}$
where
${{A}_{A}}$ is the area of the cross-section at $A$
${{V}_{A}}$ is the speed of the water at $A$
${{A}_{B}}$ is the area of the cross-section at $B$
${{V}_{B}}$ is the speed of the water at $B$
Let this be equation 1.
Substituting the given values from the question in equation 1, we have
${{A}_{A}}{{V}_{A}}={{A}_{B}}{{V}_{B}}\Rightarrow 1c{{m}^{3}}\times 10cm{{s}^{-1}}=0.5c{{m}^{3}}\times {{V}_{B}}\Rightarrow {{V}_{B}}=\dfrac{1c{{m}^{3}}\times 10cm{{s}^{-1}}}{0.5c{{m}^{3}}}=20cm{{s}^{-1}}$
where
${{A}_{A}}=1c{{m}^{3}}$ is the area of cross-section at $A$
${{V}_{A}}=10cm{{s}^{-1}}$ is the speed of water at $A$
${{A}_{B}}=0.5c{{m}^{3}}$ is the area of cross-section at $B$
${{V}_{B}}$ is the speed of water at $B$
Let this be equation 2.
Now, we know that Bernoulli’s theorem for water flow suggests that pressure difference between $A$ and $B$ is dependent on the difference in speeds of water at $A$ and $B$, height difference between $A$ and $B$, density of water and acceleration due to gravity. Mathematically, Bernoulli’s theorem can be expressed as
${{P}_{A}}+\dfrac{1}{2}\rho {{V}_{A}}^{2}+\rho g{{h}_{A}}={{P}_{B}}+\dfrac{1}{2}\rho {{V}_{B}}^{2}+\rho g{{h}_{B}}\Rightarrow {{P}_{B}}-{{P}_{A}}=\dfrac{1}{2}\rho \left( {{V}_{A}}^{2}-{{V}_{B}}^{2} \right)+\rho g\left( {{h}_{A}}-{{h}_{B}} \right)$
where
${{P}_{A}}$ is the pressure at $A$
${{V}_{A}}$ is the speed of water at $A$
${{P}_{B}}$ is the pressure at $B$
${{V}_{B}}$ is the speed of water at $B$
${{h}_{A}}-{{h}_{B}}$ is the height difference between $A$ and $B$
$\rho $ is the density of water
$g$ is the acceleration due to gravity
Let this be equation 3.
Substituting the values given in the question and equation 2 in equation 3, we have
${{P}_{B}}-{{P}_{A}}=\dfrac{1}{2}\rho \left( {{V}_{A}}^{2}-{{V}_{B}}^{2} \right)+\rho g\left( {{h}_{A}}-{{h}_{B}} \right)=\dfrac{1}{2}{{10}^{3}}kg{{m}^{-3}}\left( {{\left( 10cm{{s}^{-1}} \right)}^{2}}-{{\left( 20cm{{s}^{-1}} \right)}^{2}} \right)+({{10}^{3}}kg{{m}^{-3}})(10m{{s}^{-2}})\left( 5cm \right)$
Simplifying the above expression, we have
\[{{P}_{B}}-{{P}_{A}}=\dfrac{1}{2}{{10}^{3}}kg{{m}^{-3}}\left( -0.03{{m}^{2}}{{s}^{-2}} \right)+500kg{{m}^{-1}}{{s}^{-2}}=-15kg{{m}^{-1}}{{s}^{-2}}+500kg{{m}^{-1}}{{s}^{-2}}=485Pa\]
Let this be equation 4.
Therefore, from equation 2 and equation 4, the speed of the water at $B$ and the pressure difference between $A$ and $B$ are $20cm{{s}^{-1}}$ and $485Pa$.
Note: Students need to be aware of the continuity equation as well as Bernoulli’s theorem for solving this question in no time. They need to be thorough with conversion formulas too. Conversion formulas used in the solution given above are
\[\begin{align}
& 1m={{10}^{2}}cm \\
& 1cm{{s}^{-1}}={{10}^{-2}}m{{s}^{-1}} \\
& 1c{{m}^{2}}{{s}^{-2}}={{10}^{-4}}{{m}^{2}}{{s}^{-2}} \\
& 1Pa=1kg{{m}^{-1}}{{s}^{-2}} \\
& \\
\end{align}\]
Also, the values of acceleration due to gravity $(g)$ and density of water $(\rho )$ are taken as $10m{{s}^{-2}}$ and $10kg{{m}^{-3}}$, respectively.
Formula used:
$\begin{align}
& 1){{A}_{A}}{{V}_{A}}={{A}_{B}}{{V}_{B}} \\
& 2){{P}_{A}}+\dfrac{1}{2}\rho {{V}_{A}}^{2}+\rho g{{h}_{A}}={{P}_{B}}+\dfrac{1}{2}\rho {{V}_{B}}^{2}+\rho g{{h}_{B}} \\
\end{align}$
Complete step-by-step solution
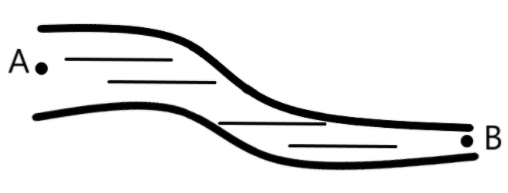
We are provided with the case of water flow in a tube, as shown in the following figure.

The area of cross-section at $A$ and $B$ are $1c{{m}^{3}}$ and $0.5c{{m}^{3}}$ respectively and the height difference between $A$ and $B$ is $5cm$. If the speed of the water at $A$ is $10cm{{s}^{-1}}$, we are required to find the speed of the water at $B$ and the difference in pressure at $A$ and $B$.
From the continuity equation of water flow, we know that the product of the speed of water and area of the cross-section at $A$ is equal to the product of the speed of water and area of the cross-section at $B$. Mathematically, the equation of continuity is given by
${{A}_{A}}{{V}_{A}}={{A}_{B}}{{V}_{B}}$
where
${{A}_{A}}$ is the area of the cross-section at $A$
${{V}_{A}}$ is the speed of the water at $A$
${{A}_{B}}$ is the area of the cross-section at $B$
${{V}_{B}}$ is the speed of the water at $B$
Let this be equation 1.
Substituting the given values from the question in equation 1, we have
${{A}_{A}}{{V}_{A}}={{A}_{B}}{{V}_{B}}\Rightarrow 1c{{m}^{3}}\times 10cm{{s}^{-1}}=0.5c{{m}^{3}}\times {{V}_{B}}\Rightarrow {{V}_{B}}=\dfrac{1c{{m}^{3}}\times 10cm{{s}^{-1}}}{0.5c{{m}^{3}}}=20cm{{s}^{-1}}$
where
${{A}_{A}}=1c{{m}^{3}}$ is the area of cross-section at $A$
${{V}_{A}}=10cm{{s}^{-1}}$ is the speed of water at $A$
${{A}_{B}}=0.5c{{m}^{3}}$ is the area of cross-section at $B$
${{V}_{B}}$ is the speed of water at $B$
Let this be equation 2.
Now, we know that Bernoulli’s theorem for water flow suggests that pressure difference between $A$ and $B$ is dependent on the difference in speeds of water at $A$ and $B$, height difference between $A$ and $B$, density of water and acceleration due to gravity. Mathematically, Bernoulli’s theorem can be expressed as
${{P}_{A}}+\dfrac{1}{2}\rho {{V}_{A}}^{2}+\rho g{{h}_{A}}={{P}_{B}}+\dfrac{1}{2}\rho {{V}_{B}}^{2}+\rho g{{h}_{B}}\Rightarrow {{P}_{B}}-{{P}_{A}}=\dfrac{1}{2}\rho \left( {{V}_{A}}^{2}-{{V}_{B}}^{2} \right)+\rho g\left( {{h}_{A}}-{{h}_{B}} \right)$
where
${{P}_{A}}$ is the pressure at $A$
${{V}_{A}}$ is the speed of water at $A$
${{P}_{B}}$ is the pressure at $B$
${{V}_{B}}$ is the speed of water at $B$
${{h}_{A}}-{{h}_{B}}$ is the height difference between $A$ and $B$
$\rho $ is the density of water
$g$ is the acceleration due to gravity
Let this be equation 3.
Substituting the values given in the question and equation 2 in equation 3, we have
${{P}_{B}}-{{P}_{A}}=\dfrac{1}{2}\rho \left( {{V}_{A}}^{2}-{{V}_{B}}^{2} \right)+\rho g\left( {{h}_{A}}-{{h}_{B}} \right)=\dfrac{1}{2}{{10}^{3}}kg{{m}^{-3}}\left( {{\left( 10cm{{s}^{-1}} \right)}^{2}}-{{\left( 20cm{{s}^{-1}} \right)}^{2}} \right)+({{10}^{3}}kg{{m}^{-3}})(10m{{s}^{-2}})\left( 5cm \right)$
Simplifying the above expression, we have
\[{{P}_{B}}-{{P}_{A}}=\dfrac{1}{2}{{10}^{3}}kg{{m}^{-3}}\left( -0.03{{m}^{2}}{{s}^{-2}} \right)+500kg{{m}^{-1}}{{s}^{-2}}=-15kg{{m}^{-1}}{{s}^{-2}}+500kg{{m}^{-1}}{{s}^{-2}}=485Pa\]
Let this be equation 4.
Therefore, from equation 2 and equation 4, the speed of the water at $B$ and the pressure difference between $A$ and $B$ are $20cm{{s}^{-1}}$ and $485Pa$.
Note: Students need to be aware of the continuity equation as well as Bernoulli’s theorem for solving this question in no time. They need to be thorough with conversion formulas too. Conversion formulas used in the solution given above are
\[\begin{align}
& 1m={{10}^{2}}cm \\
& 1cm{{s}^{-1}}={{10}^{-2}}m{{s}^{-1}} \\
& 1c{{m}^{2}}{{s}^{-2}}={{10}^{-4}}{{m}^{2}}{{s}^{-2}} \\
& 1Pa=1kg{{m}^{-1}}{{s}^{-2}} \\
& \\
\end{align}\]
Also, the values of acceleration due to gravity $(g)$ and density of water $(\rho )$ are taken as $10m{{s}^{-2}}$ and $10kg{{m}^{-3}}$, respectively.
Recently Updated Pages
The correct geometry and hybridization for XeF4 are class 11 chemistry CBSE

Water softening by Clarks process uses ACalcium bicarbonate class 11 chemistry CBSE

With reference to graphite and diamond which of the class 11 chemistry CBSE

A certain household has consumed 250 units of energy class 11 physics CBSE

The lightest metal known is A beryllium B lithium C class 11 chemistry CBSE

What is the formula mass of the iodine molecule class 11 chemistry CBSE

Trending doubts
State the laws of reflection of light

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

How do I convert ms to kmh Give an example class 11 physics CBSE

Give an example of a solid solution in which the solute class 11 chemistry CBSE

Describe the effects of the Second World War class 11 social science CBSE




