Question

Water is dripping out from a conical funnel at the uniform rate of $4c{m^3}/{\text{sec}}$ . When the slant height of the water is $3cm$ , find the rate of the decrease of the slant height of the water, given that the vertical angle of the funnel is ${120^ \circ }$ .

Answer 1

Hint: Apply the derivative methods. Rate of decrease of volume is given to us. Use that information.

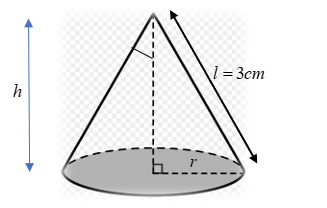
It’s given that the vertical angle is ${120^ \circ }$ so half of it will be ${60^ \circ }$ . Slant height l is given to us as $3cm$ . Let the height be h and radius be r. The question says, water is dripping out from a conical funnel at the uniform rate of $4c{m^3}/{\text{sec}}$ . In case of a full canonical funnel with water, we say volume is equal to the water present in the funnel. Since, water is decreasing with the uniform rate then we can say $\dfrac{{dV}}{{dt}} = - 4$ . The unit $c{m^3}/{\text{sec}}$ also confirms the fact that it’s nothing but volume. One might think that why the negative sign we are taking? It's because of the fact that the water is decreasing by time. For that decrement, we are using negative signs. Now,
 $
  \sin {60^ \circ } = \dfrac{r}{l} \Rightarrow \dfrac{{\sqrt 3 }}{2} = \dfrac{r}{l} \Rightarrow r = \dfrac{{\sqrt 3 l}}{2} \\
  \cos {60^ \circ } = \dfrac{h}{l} \Rightarrow \dfrac{1}{2} = \dfrac{h}{l} \Rightarrow h = \dfrac{l}{2} \\
$
We know the formula for volume of the cone,
\[
  V = \dfrac{1}{3}\pi {r^2}h \\
   \Rightarrow V = \dfrac{1}{3}\pi {(\dfrac{{\sqrt 3 l}}{2})^2}\dfrac{l}{2}{\text{ }}[r = \dfrac{{\sqrt 3 l}}{2},h = \dfrac{l}{2}] \\
   \Rightarrow V = \dfrac{1}{{{3}}} \times \pi \times \dfrac{{{3}{l^2}}}{4} \times \dfrac{l}{2} \\
   \Rightarrow V = \dfrac{1}{8}\pi {l^3} \\
\]
On differentiating we’ll be getting,
$
  \dfrac{{dV}}{{dt}} = \dfrac{\pi }{8}3{l^2}\dfrac{{dl}}{{dt}} \\
   \Rightarrow - 4 = \dfrac{\pi }{8}3{(3)^2}\dfrac{{dl}}{{dt}}{\text{ }}[\dfrac{{dV}}{{dt}} = - 4c{m^3}/\sec ,l = 3 cm] \\
   \Rightarrow \dfrac{{dl}}{{dt}} = \dfrac{{ - 4 \times 8}}{{27\pi }} \\
   \Rightarrow \dfrac{{dl}}{{dt}} = \dfrac{{ - 32}}{{27\pi }} \\
$
Hence, the rate of the decrease of the slant height of the water is $\dfrac{{ - 32}}{{27\pi }}$ .
Note: The toughest part in this question is to recognise the concept. Once you get it as the question of rates then half of the question is finished there itself. After that, we need to find the rate given to us and then use its formula. It’ll lead us to the solution.