Answer
Verified409.5k+ views
Hint: We shall first understand the individual meaning of these terms. The term ‘v’ is defined as the instantaneous velocity, ‘dx’ being instantaneous change in displacement and ‘dt’ being the very small instant of time. Thus, the above term is a mathematical representation of instantaneous velocity of a particle having a certain displacement. Let us understand it in detail.
Complete step-by-step solution:
Let there be a particle whose equation of motion is defined collectively by the term ‘x’. This motion can be a straight-line motion, circular, motion in 3D with variable acceleration, anything.
Now, the expression that has been given to us, that is, $v=\dfrac{dx}{dt}$ is a differential of this motion of the particle with respect to time. Thus, the term ‘v’ comes out to be its instantaneous velocity. Also, this could be understood graphically as follows:
At first let us suppose a particle has the following displacement-time curve:
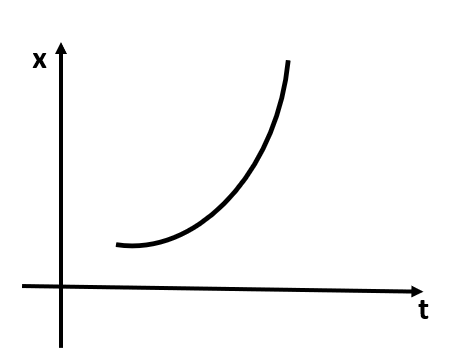
Then, the velocity of any particle at an instant can be given as the slope of this curve at that instant. This can be graphically represented as follows:
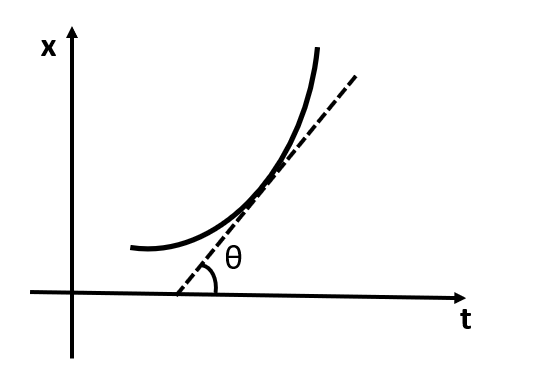
Here, the slope of the curve, that is equal to $\tan \theta $ gives us the instantaneous velocity of the particle.
Hence, the term, $v=\dfrac{dx}{dt}$ means that it is a mathematical representation of instantaneous velocity of a particle under motion.
Note: If we further differentiate the term for velocity with respect to time, we will get the mathematical representation of instantaneous acceleration, that is, $a=\dfrac{dv}{dt}$, which is also equal to, $a=\dfrac{{{d}^{2}}x}{d{{t}^{2}}}$ . Hence, acceleration of the particle is obtained by double differentiation of the displacement of the respective particle.
Complete step-by-step solution:
Let there be a particle whose equation of motion is defined collectively by the term ‘x’. This motion can be a straight-line motion, circular, motion in 3D with variable acceleration, anything.
Now, the expression that has been given to us, that is, $v=\dfrac{dx}{dt}$ is a differential of this motion of the particle with respect to time. Thus, the term ‘v’ comes out to be its instantaneous velocity. Also, this could be understood graphically as follows:
At first let us suppose a particle has the following displacement-time curve:
Then, the velocity of any particle at an instant can be given as the slope of this curve at that instant. This can be graphically represented as follows:
Here, the slope of the curve, that is equal to $\tan \theta $ gives us the instantaneous velocity of the particle.
Hence, the term, $v=\dfrac{dx}{dt}$ means that it is a mathematical representation of instantaneous velocity of a particle under motion.
Note: If we further differentiate the term for velocity with respect to time, we will get the mathematical representation of instantaneous acceleration, that is, $a=\dfrac{dv}{dt}$, which is also equal to, $a=\dfrac{{{d}^{2}}x}{d{{t}^{2}}}$ . Hence, acceleration of the particle is obtained by double differentiation of the displacement of the respective particle.