Question

What is incenter?

Answer 1

Hint: When we face such questions, the first step is to draw a triangle, say ABC. Now, ‘incentre’ gives us a hint that there is a circle involved. So think and draw the circle either outside or inside the triangle. Then consider the internal angle bisectors of the triangle ABC which will intersect at a point, which is equidistant from the sides of the triangle. You will then get the incenter.

Complete step by step solution:
Let us first draw the figure. We will draw a triangle and mark the vertices as ABC. We can also mark the sides as a, b, c. Now, from the term incentre, we get the idea that a circle is inscribed inside the triangle that we have just drawn. Now, we have to look into the definition of incentre.
The incenter of a triangle is the center of the triangle, a point defined for any triangle in a way that is independent of the triangle’s placement. So we can say that if we draw the angle bisectors of all the three angles of the triangle, we will get a common point where they will intersect. That point can be named as incentre. Also all sides of the triangle will be equidistant from this point.
Let C be the length of AB, ‘a’ be the length of BC and b be the length of AC.

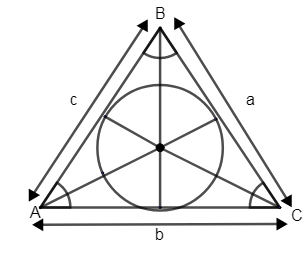
We have the cartesian coordinates of the incenter are a weighted average of the coordinates of the three vertices using the side lengths of the triangle relative to the perimeter. Let us consider the three vertices are A (\[{{x}_{A}},{{y}_{A}}\]), B (\[{{x}_{B}},{{y}_{B}}\]), C (\[{{x}_{C}},{{y}_{C}}\]) and the side opposite to the three vertices have corresponding lengths a, b and c then the incenter is at,
\[\left( \dfrac{a{{x}_{A}}+b{{x}_{B}}+c{{x}_{C}}}{a+b+c},\dfrac{a{{y}_{A}}+b{{y}_{B}}+c{{y}_{C}}}{a+b+c} \right)\]
Thus we learned that incenter is the center of the triangle and the formula to find the incenter when we know the lengths of sides of the triangle.

Note: Apart from incenter there is centroid, circumcenter and orthocenter in a triangle. Together it is one of four triangle centers known to the ancient Greeks, and the only one that does not in general lie on the Euler’s line i.e. line determined from any triangle that is not equilateral. Sometimes students get confused with the terms incenter and orthocenter. Orthocenter is the point where all the three altitudes of the triangle meet. So this difference must be kept in mind while answering the question.