
What is the angle of twist?
Answer
408.9k+ views
Hint:Torsion is the twisting of an object caused by a moment acting about the object’s longitudinal axis. This is a type of deformation. A moment that tends to cause is called torque. If we apply a torque to a circular bar with one end fixed, the torque causes the free end to deform or rotate through an angle this angle is called the Angle of twist.
Formula Used
Complete step by step solution:
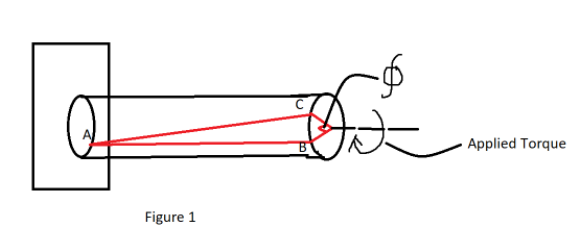
From figure 1 we can see that if we apply torque to a cylindrical bar it causes the bar to deform by twisting. The above cylindrical bar is fixed at one end and the other is left free. While applying the torque if we notice the line AB, the line rotates by angle Phi
We can calculate the angle of twist from the following equation.
Where
Note:The polar moment of inertia is the object’s capacity to resist the internal torque which is applied to the circular bar.
The angle of twist is usually measured in radians. But in the end, they will be converted to degrees.
The shear modulus G is the material’s property. In some cases, the above formula can be rearranged to find the material’s shear modulus.
The general formula for the angle of twist is given below
Formula:
Formula Used
Complete step by step solution:

From figure 1 we can see that if we apply torque to a cylindrical bar it causes the bar to deform by twisting. The above cylindrical bar is fixed at one end and the other is left free. While applying the torque if we notice the line AB, the line rotates by angle Phi
We can calculate the angle of twist from the following equation.
Where
Note:The polar moment of inertia is the object’s capacity to resist the internal torque which is applied to the circular bar.
The angle of twist is usually measured in radians. But in the end, they will be converted to degrees.
The shear modulus G is the material’s property. In some cases, the above formula can be rearranged to find the material’s shear modulus.
The general formula for the angle of twist is given below
Formula:
Recently Updated Pages
Express the following as a fraction and simplify a class 7 maths CBSE

The length and width of a rectangle are in ratio of class 7 maths CBSE

The ratio of the income to the expenditure of a family class 7 maths CBSE

How do you write 025 million in scientific notatio class 7 maths CBSE

How do you convert 295 meters per second to kilometers class 7 maths CBSE

Write the following in Roman numerals 25819 class 7 maths CBSE

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

What are Quantum numbers Explain the quantum number class 11 chemistry CBSE

Write the differences between monocot plants and dicot class 11 biology CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light

In northern hemisphere 21st March is called as A Vernal class 11 social science CBSE




