Question

What is the ellipse shape?

Answer 1

Hint: An ellipse is a plane curve surrounding two focal points, such that for all points on the curve, the sum of the two distances to the focal points is a constant. As such, it generalizes a circle, which is the special type of ellipse in which the two focal points are the same.

Complete step-by-step solution:
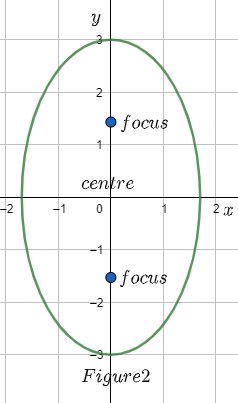
We know that an ellipse is a shape that looks like an oval or a flattened circle. An ellipse is the set of all points in a plane the sum of whose distance from two fixed points, called the foci, is a constant. We can say that a circle is a special type of ellipse where both focal points are at the same point, the centre. We have two types of ellipses and are shown below:

Now, let us understand the terms. So, in Figure 1, the x-axis is called the major axis and the y-axis is called the minor axis. We call it so because the ellipse is stretched or larger in the x-direction.
When we look at Figure 2, the y-axis is called the major axis and the x-axis is called the minor axis because the ellipse is stretched or larger in the y-direction. It is very important for us to determine which axis is the major axis because the vertices, V, and the foci, F, are always located on the major axis.
We know that there are two equations for an ellipse with the centre at the origin, (0, 0). We have them as
\[\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1\] ….(1)
In the equation (1), we can identify the x-axis as the major axis because the bigger number, a, is below x.
\[\dfrac{{{x^2}}}{{{b^2}}} + \dfrac{{{y^2}}}{{{a^2}}} = 1\] ….(2)
In the equation (2), we can identify the y-axis as the major axis because the bigger number, a, is below y.
Where, a = the distance from the centre, C, to the vertex, V .
b = the distance from the centre, C, to the other side.

Note: Ellipse is similar to other parts of the conic section such as parabola and hyperbola, which are open in shape and unbounded. When an ellipse is written in standard form, the major axis direction is determined by noting which variable has the larger denominator. The major axis either lies along that variable's axis or is parallel to that variable's axis. Similarly, we can have questions for hyperbola also.