Question

What is the perpendicular slope of 3?

Answer 1

Hint: The given slope of the line is 3. We can find the perpendicular slope of this line by finding the slope of the line which is perpendicular to the original line. Let ${{m}_{1}}$ be the slope of the first line and let ${{m}_{2}}$ be the slope of the second line or the line perpendicular to the first line. We can find the slope of the line perpendicular to the original line by using the formula,
$\begin{align}
& \,{{m}_{1}}{{m}_{2}}=-1 \\
& \Rightarrow {{m}_{2}}=-\dfrac{1}{{{m}_{1}}} \\
\end{align}$

Complete step-by-step solution:

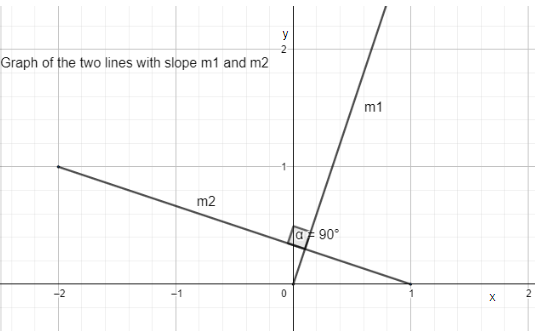
The slope of a straight line is defined as the ratio of the change in y-coordinate of the line to the change in x-coordinate of the line. Slope can also be defined as the tangent of the angle made by the line with the x-axis. If two lines are perpendicular, it implies they intersect at ${{90}^{\circ }}$ at the point of intersection.
Let us assume ${{m}_{1}}$ to be the slope of the first line or the line given to us in the question. Hence we can see that ${{m}_{1}}=3$ , is given to us in the question. Let us assume ${{m}_{2}}$ to be the slope of the second line or the line which is perpendicular to the given line. We can find the slope of the second line by using the formula for two perpendicular lines in Cartesian plane, which is,
$\begin{align}
  & \,{{m}_{1}}{{m}_{2}}=-1 \\
 & \Rightarrow {{m}_{2}}=-\dfrac{1}{{{m}_{1}}} \\
\end{align}$
Therefore, we get,
${{m}_{2}}=-\dfrac{1}{3}$
The slope of the line perpendicular to 3 is $-\dfrac{1}{3}$ .

Note: While the formula for slope of two perpendicular lines works well for almost all cases, one should be careful when the slope of a line is given as 0. In this case we get,
$\begin{align}
  & {{m}_{2}}=-\dfrac{1}{{{m}_{1}}} \\
 & {{m}_{2}}=-\dfrac{1}{0} \\
\end{align}$
Which means that ${{m}_{2}}$ is infinity. In reality, this means that the line is vertical since the inverse tangent of infinity is ${{90}^{\circ }}$ which means it is perpendicular to x-axis and parallel with the y-axis. Any line parallel to the y-axis and perpendicular to x-axis will have a slope of infinity.