
What is the square root of \[8{{x}^{2}}\] ?
Answer
412.2k+ views
Hint: We are given to find the square root of \[8{{x}^{2}}\]. Firstly, we check whether the given number is a perfect square or not. We can find it by either long division or by prime factorization method. Square root exists only when a number is a perfect square. The square root can be either positive or negative because the product of two negative numbers is also a positive number.
Complete step-by-step solution:
Let us learn about square roots now. The square root is nothing but the number when squared or multiplied itself gives the original number. When a number is a perfect square, the perfect square root exists for that number. The square root of any negative number is undefined.
Now let us find the square root of \[8{{x}^{2}}\].
This can be expressed as \[\sqrt{8{{x}^{2}}}\]
Now upon computing it, we get
\[\sqrt{8{{x}^{2}}}=\sqrt{{{2}^{2}}\times 2\times {{x}^{2}}}\]
Now let us split the terms, we get
\[\Rightarrow \sqrt{{{2}^{2}}}\times \sqrt{2}\times \sqrt{{{x}^{2}}}\]
Now, upon taking the squares outside the root as the roots and squares gets cancelled, we get,
\[\Rightarrow 2\sqrt{2}x\]
We can rearrange this and rewrite it as \[2x\sqrt{2}\].
\[\therefore \] The square root of \[8{{x}^{2}}\] is \[2x\sqrt{2}\].
Note: All non-zero numbers have only one real root. This method of prime factorization breaks down the number into sub parts which makes it easier for finding the root of the number. A perfect square cannot be negative
Now let us plot this upon the graph.
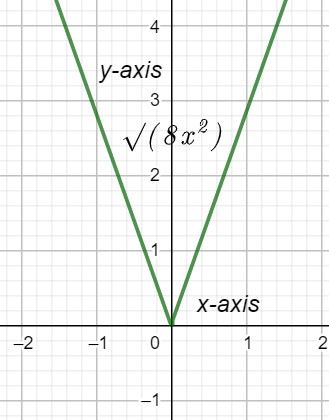
Complete step-by-step solution:
Let us learn about square roots now. The square root is nothing but the number when squared or multiplied itself gives the original number. When a number is a perfect square, the perfect square root exists for that number. The square root of any negative number is undefined.
Now let us find the square root of \[8{{x}^{2}}\].
This can be expressed as \[\sqrt{8{{x}^{2}}}\]
Now upon computing it, we get
\[\sqrt{8{{x}^{2}}}=\sqrt{{{2}^{2}}\times 2\times {{x}^{2}}}\]
Now let us split the terms, we get
\[\Rightarrow \sqrt{{{2}^{2}}}\times \sqrt{2}\times \sqrt{{{x}^{2}}}\]
Now, upon taking the squares outside the root as the roots and squares gets cancelled, we get,
\[\Rightarrow 2\sqrt{2}x\]
We can rearrange this and rewrite it as \[2x\sqrt{2}\].
\[\therefore \] The square root of \[8{{x}^{2}}\] is \[2x\sqrt{2}\].
Note: All non-zero numbers have only one real root. This method of prime factorization breaks down the number into sub parts which makes it easier for finding the root of the number. A perfect square cannot be negative
Now let us plot this upon the graph.

Recently Updated Pages
Master Class 11 Accountancy: Engaging Questions & Answers for Success

Express the following as a fraction and simplify a class 7 maths CBSE

The length and width of a rectangle are in ratio of class 7 maths CBSE

The ratio of the income to the expenditure of a family class 7 maths CBSE

How do you write 025 million in scientific notatio class 7 maths CBSE

How do you convert 295 meters per second to kilometers class 7 maths CBSE

Trending doubts
When people say No pun intended what does that mea class 8 english CBSE

How many ounces are in 500 mL class 8 maths CBSE

In Indian rupees 1 trillion is equal to how many c class 8 maths CBSE

Which king started the organization of the Kumbh fair class 8 social science CBSE

What is BLO What is the full form of BLO class 8 social science CBSE

Advantages and disadvantages of science




