Question

Wheatstone’s bridge cannot be used for measurement of very _____ resistances.
A) high
B) low
C) low (or) high
D) zero

Answer 1

Hint: We need to know the Wheatstone’s bridge condition to analyse and understand the types (low or high) of resistances it can measure using the condition. The Wheatstone’s bridge condition is a direct consequence of Kirchhoff's loop rule.

Complete step by step solution:
The Wheatstone’s bridge condition is a secondary condition derived from Kirchhoff's loop rule. According to the loop rule, the total algebraic sum of the potential drops across the resistors in the circuit is equal to the emf provided in the circuit.
i.e.,
\[\begin{align}
  & \varepsilon ={{V}_{1}}+{{V}_{2}}+{{V}_{3}}+...+{{V}_{n}} \\
 & \therefore \varepsilon -({{V}_{1}}+{{V}_{2}}+{{V}_{3}}+...+{{V}_{n}})=0 \\
\end{align}\]
Where, n is the number of resistances in the circuit.
The Kirchhoff’s loop rule can directly give a conclusion that there will be no current flow between two points which are at the same potential. This is the governing condition of the Wheatstone’s bridge.

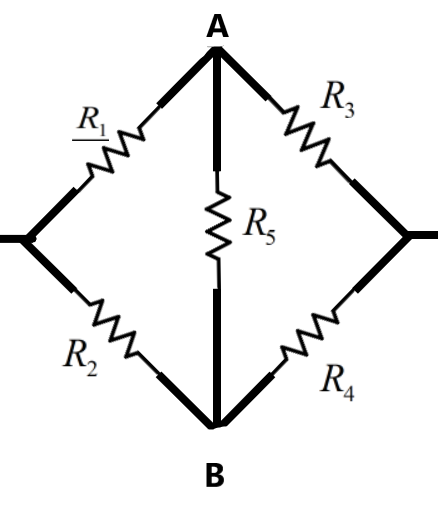
According to the Wheatstone’s bridge condition, for a circuit consisting of a combination of resistances as shown below, the current flowing through the resistor \[{{R}_{5}}\] will be zero, if the resistances on the two opposite hands in the circuit are in the same ratio as –
\[\dfrac{{{R}_{1}}}{{{R}_{2}}}=\dfrac{{{R}_{3}}}{{{R}_{4}}}\]
This is Wheatstone's condition.
Now, we can understand that the Wheatstone’s condition is highly sensitive to the resistances present in the circuit. A minute change in the resistance of any of the resistors can make the bridge unbalanced. That means, the resistance of the circuit elements should be treated very carefully. Measuring very low resistances using the bridge can give erroneous results due to resistance offered by the wires, the devices like galvanometer, internal resistance of the cell and other elements in the circuit.
So, the low resistances when measured using a Wheatstone’s condition will give unfavourable answers.

The correct answer is option B.

Note:
The Wheatstone’ bridge condition is the working principle behind the meter bridge. In the meter bridge, the length of the wire balances the resistance and forms the potential at the two points to be zero. This gives the null deflection on the galvanometer.