Question

Which figure has an area of 20 sq. units and a perimeter of 18 units?
(a)

(b)

(c)

(d)

Answer 1

Hint: Here in the given problem, we are trying to find the figure with 20 sq. units area and 18 units of perimeter. And easily we can also see that the figures are made of unit squares with area 1 sq units. So, to find the total area we are going to count the number of squares and then try to find the perimeter with the formula of the rectangle’s perimeter.

Complete step-by-step solution:
According to the problem, we are to find the figure with an area of 20 sq. units and a perimeter of 18 units.
Here, we can easily see that the given figures consist of boxes with the same size and same area. And also, the area of a single square is = $1\times 1$sq. unit.
Which means each of them is a single unit square.
Now, we will check the options one by one to find out which one satisfies the given condition in the problem and find the right one.
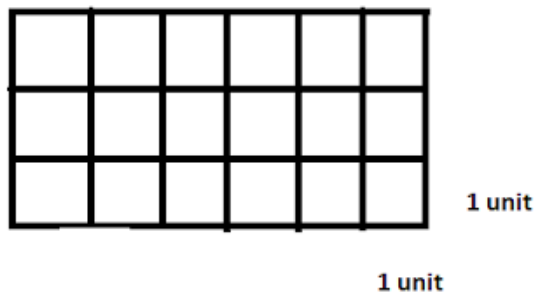
In the first option, we can see, there are 18 squares. So, the total area is 18 sq. unit.
And for the perimeter, as it is a rectangle, with sides 3 and 6 units respectively, we are getting the area as $2\times \left( 6+3 \right)$ $=18$ units. So, this is a wrong option.
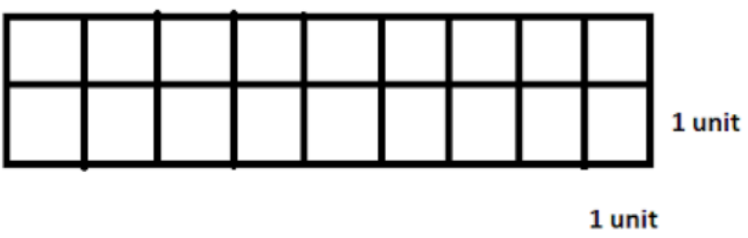
In the second option, we can see, there are also 18 squares. So, the total area is 18 sq. unit.
And for the perimeter, as it is also a rectangle, with sides 2 and 9 units respectively, we are getting the area as $2\times \left( 9+2 \right)$ $=22$ units. So, this is also a wrong option.
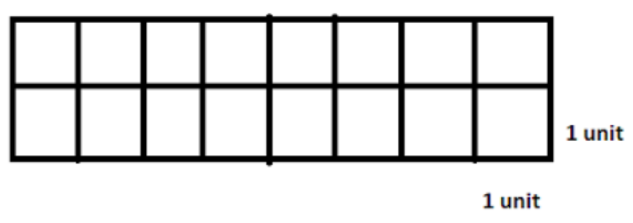
Again, In the third option, we can see, there are 16 squares. So, the total area is 16 sq. unit.
And for the perimeter, as it is a rectangle, with sides 2 and 8 units respectively, we are getting the area as $2\times \left( 8+2 \right)$ $=20$ units. So, this is again a wrong option.
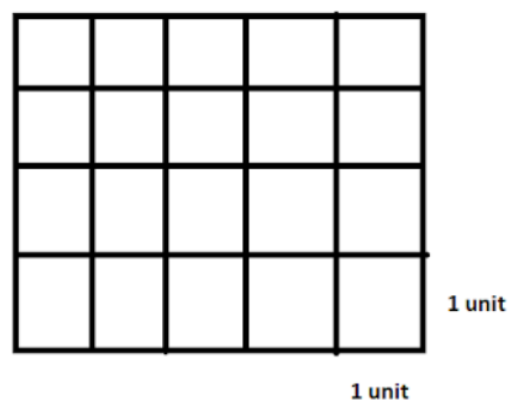
For, the fourth option, we get, there are 20 squares. So, the total area is 20 sq. unit.
And for the perimeter, as it is a rectangle, with sides 4 and 5 units respectively, we are getting the area as $2\times \left( 5+4 \right)$ $=18$ units. So, this is the correct option.

Note: This is a problem which can be placed in many ways like finding the numbers of squares in the figure or finding the figure with the largest area. For each case, we will follow the same way to reach the area and perimeter of each figure. And, then, we will analyze the given conditions to reach our desired solution.