
Which of the following are correct regarding the normal distribution curve?
(i) Symmetrical about line $X = \mu $ (Mean)
(ii) Mean = Median = Mode
(iii) Unimodal
(iv) Points of inflexion are at $X = \mu \pm \sigma $
A) (i), (ii)
B) (ii), (iv)
C) (i), (ii), (iii)
D) All of these
Answer
216.6k+ views
Hint:
In the given question, we are asked to find what is correct regarding the normal distribution curve. By looking at the properties of the normal distributive, the given question can be solved easily. Find out which points are correct in regards to the normal distribution curve.
Thus, choose the correct option.
Complete step by step solution:
In the given question, we are asked to find which of the following is correct regarding the normal distribution curve.
Symmetrical about line $X = \mu $ (Mean)
Mean = Median = Mode
Unimodal
Points of inflexion are at $X = \mu \pm \sigma $
In a normal distribution, the values of mean, median and mode are equal. So, the point (ii) is correct in the context of a normal distribution curve.
Also, the normal distribution curve or bell curve is symmetric about the line $X = \mu $ . So, the point (i) is also correct in this context.
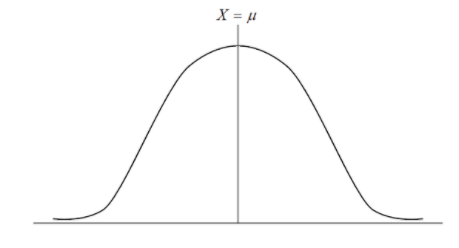
Now, for a normal curve to be Unimodal the first derivative must be 0 at $X = \mu $ and it must be less than 0 for $X > \mu $ and greater than 0 for $X < \mu $ , which is the exact case here. So, point (iii) is also correct.
For points of inflexion, the second derivative must be 0 at those points. Here, the second derivative is 0 at $X = \mu + \sigma $ and $X = \mu - \sigma $ . So, the points of inflexion are $X = \mu \pm \sigma $. Thus, point (iv) is also correct.
Hence, option (D) is the correct answer as all the given four points are correct in the context of a normal distribution curve.
Note:
Properties of a normal distribution curve:
i) The mean, mode and median are all equal.
ii) The curve is symmetric at the centre, i.e. around mean $\mu $.
iii) Exactly half of the values are to the left of centre and exactly half the values are to the right.
iv) The total area under the curve is 1.
In the given question, we are asked to find what is correct regarding the normal distribution curve. By looking at the properties of the normal distributive, the given question can be solved easily. Find out which points are correct in regards to the normal distribution curve.
Thus, choose the correct option.
Complete step by step solution:
In the given question, we are asked to find which of the following is correct regarding the normal distribution curve.
Symmetrical about line $X = \mu $ (Mean)
Mean = Median = Mode
Unimodal
Points of inflexion are at $X = \mu \pm \sigma $
In a normal distribution, the values of mean, median and mode are equal. So, the point (ii) is correct in the context of a normal distribution curve.
Also, the normal distribution curve or bell curve is symmetric about the line $X = \mu $ . So, the point (i) is also correct in this context.

Now, for a normal curve to be Unimodal the first derivative must be 0 at $X = \mu $ and it must be less than 0 for $X > \mu $ and greater than 0 for $X < \mu $ , which is the exact case here. So, point (iii) is also correct.
For points of inflexion, the second derivative must be 0 at those points. Here, the second derivative is 0 at $X = \mu + \sigma $ and $X = \mu - \sigma $ . So, the points of inflexion are $X = \mu \pm \sigma $. Thus, point (iv) is also correct.
Hence, option (D) is the correct answer as all the given four points are correct in the context of a normal distribution curve.
Note:
Properties of a normal distribution curve:
i) The mean, mode and median are all equal.
ii) The curve is symmetric at the centre, i.e. around mean $\mu $.
iii) Exactly half of the values are to the left of centre and exactly half the values are to the right.
iv) The total area under the curve is 1.
Recently Updated Pages
JEE Repeater course 2026 for Class 12

JEE Atomic Structure and Chemical Bonding important Concepts and Tips

JEE Amino Acids and Peptides Important Concepts and Tips for Exam Preparation

Electricity and Magnetism Explained: Key Concepts & Applications

Chemical Properties of Hydrogen - Important Concepts for JEE Exam Preparation

JEE Energetics Important Concepts and Tips for Exam Preparation

Trending doubts
JEE Main 2026: Application Form Open, Exam Dates, Syllabus, Eligibility & Question Papers

Derivation of Equation of Trajectory Explained for Students

Hybridisation in Chemistry – Concept, Types & Applications

Understanding the Angle of Deviation in a Prism

Understanding Collisions: Types and Examples for Students

How to Convert a Galvanometer into an Ammeter or Voltmeter

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Ideal and Non-Ideal Solutions Explained for Class 12 Chemistry

Degree of Dissociation: Meaning, Formula, Calculation & Uses

Understanding Electromagnetic Waves and Their Importance

Understanding the Electric Field of a Uniformly Charged Ring

Understanding Average and RMS Value in Electrical Circuits




