
Which orbital has the highest$\dfrac{n}{k}\gg 1$value?
[A] 7s
[B] 5p
[C] 3d
[D] 4d
Answer
127.2k+ views
Hint: We can solve this question by using the Sommerfeld’s atomic model concept according to which each ‘n’ will have several values of k. We can calculate the $\dfrac{n}{k}$value for each option where ‘n’ will be the energy level and ‘k’ will be the specific s, p, d or f subshell. The highest value of $\dfrac{n}{k}$ will give us the correct answer.
Complete Step by Step Solution:
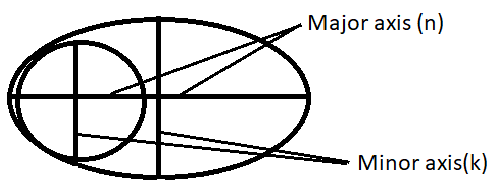
According to Sommerfeld’s atomic model, the orbitals are elliptical and corresponding to each principal quantum number (n) several orbits of varying ellipticity were possible. An ellipse has two axes major and minor and the relation between them was given as-
$\dfrac{n}{k}=\dfrac{major\text{ }axis}{minor\text{ }axis}$
Here, ‘n’ is the principal quantum number. It is the energy level to which the electron belongs and
‘k’ is the azimuthal quantum number which was later changed to ‘l’ for certain mathematical advantages.
Now we will discuss each option to find the orbital with the highest value for$\dfrac{n}{k}\gg 1$,
For s-orbital, $\dfrac{n}{k}=1$as it has a circular orbit therefore, option [A] is incorrect
In option [B], we have 5p orbital,
Here, n will be 5 and corresponding values of k will be-
K = 5 (for s-orbital), 4 (for p-orbital), 3 (for d-orbital), 2(for f-orbital) and 1 (for g-orbital)
Therefore,$\dfrac{n}{k}$for 5p-orbital will be $\dfrac{5}{4}$.
In option [C], we have a 3d orbital.
Here, n will be 3 so we can write the corresponding values of k as-
K = 3 (for s-orbital), 2 (for p-orbital), 1 (for d-orbital)
Therefore,$\dfrac{n}{k}$for 3d-orbital will be $\dfrac{3}{1}$.
In option [D] we have a 4d orbital.
Here, n will be 4 so the corresponding values of k will be –
K= 4 (for s-orbital), 3 (for p-orbital), 2(for d-orbital) and 1 (for f-orbital)
Therefore,$\dfrac{n}{k}$for 4d-orbital will be $\dfrac{4}{2}$.
As we can see from the above calculations that the value of $\dfrac{n}{k}$is highest for a 3d orbital which is 3.
Therefore, the correct answer is option [C] 3d
Note: From the above discussion, we can say that for any given value of ‘n’, k is an integer which is always greater than zero. If the major axis becomes equal to the minor axis, the orbits become circular According to this, we can write that-
If $\dfrac{n}{k}=1$, the orbit is circular and if $\dfrac{n}{k}>1$, the orbit is elliptical.
Complete Step by Step Solution:
According to Sommerfeld’s atomic model, the orbitals are elliptical and corresponding to each principal quantum number (n) several orbits of varying ellipticity were possible. An ellipse has two axes major and minor and the relation between them was given as-
$\dfrac{n}{k}=\dfrac{major\text{ }axis}{minor\text{ }axis}$
Here, ‘n’ is the principal quantum number. It is the energy level to which the electron belongs and
‘k’ is the azimuthal quantum number which was later changed to ‘l’ for certain mathematical advantages.
Now we will discuss each option to find the orbital with the highest value for$\dfrac{n}{k}\gg 1$,
For s-orbital, $\dfrac{n}{k}=1$as it has a circular orbit therefore, option [A] is incorrect
In option [B], we have 5p orbital,
Here, n will be 5 and corresponding values of k will be-
K = 5 (for s-orbital), 4 (for p-orbital), 3 (for d-orbital), 2(for f-orbital) and 1 (for g-orbital)
Therefore,$\dfrac{n}{k}$for 5p-orbital will be $\dfrac{5}{4}$.
In option [C], we have a 3d orbital.
Here, n will be 3 so we can write the corresponding values of k as-
K = 3 (for s-orbital), 2 (for p-orbital), 1 (for d-orbital)
Therefore,$\dfrac{n}{k}$for 3d-orbital will be $\dfrac{3}{1}$.
In option [D] we have a 4d orbital.
Here, n will be 4 so the corresponding values of k will be –
K= 4 (for s-orbital), 3 (for p-orbital), 2(for d-orbital) and 1 (for f-orbital)
Therefore,$\dfrac{n}{k}$for 4d-orbital will be $\dfrac{4}{2}$.
As we can see from the above calculations that the value of $\dfrac{n}{k}$is highest for a 3d orbital which is 3.
Therefore, the correct answer is option [C] 3d
Note: From the above discussion, we can say that for any given value of ‘n’, k is an integer which is always greater than zero. If the major axis becomes equal to the minor axis, the orbits become circular According to this, we can write that-
If $\dfrac{n}{k}=1$, the orbit is circular and if $\dfrac{n}{k}>1$, the orbit is elliptical.
Recently Updated Pages
JEE Main 2025 - Session 2 Registration Open | Exam Dates, Answer Key, PDF

JEE Main 2023 (January 30th Shift 2) Maths Question Paper with Answer Key

Know The Difference Between Fluid And Liquid

JEE Main 2022 (July 25th Shift 2) Physics Question Paper with Answer Key

Classification of Elements and Periodicity in Properties Chapter For JEE Main Chemistry

JEE Main 2023 (January 25th Shift 1) Maths Question Paper with Answer Key

Trending doubts
JEE Main Login 2045: Step-by-Step Instructions and Details

JEE Main Exam Marking Scheme: Detailed Breakdown of Marks and Negative Marking

JEE Main 2023 January 24 Shift 2 Question Paper with Answer Keys & Solutions

JEE Main Participating Colleges 2024 - A Complete List of Top Colleges

JEE Main Course 2025: Get All the Relevant Details

Total number of lone pair electrons in I3 ion is A class 11 chemistry JEE_Main

Other Pages
JEE Advanced 2025: Dates, Registration, Syllabus, Eligibility Criteria and More

JEE Main Chemistry Question Paper with Answer Keys and Solutions

Learn About Angle Of Deviation In Prism: JEE Main Physics 2025

Degree of Dissociation and Its Formula With Solved Example for JEE

Physics Average Value and RMS Value JEE Main 2025

What is the significance of the Heisenberg uncertainty class 11 chemistry JEE_Main




