Question

Which shape has \[12\] edges, \[8\] vertices, and \[6\] faces?

Answer 1

Hint: To solve this question, first of all we will check whether the given dimensions form a valid polyhedral or not. For this we will use Euler’s Polyhedral Formula which states that, in a convex polyhedral, if \[V\] is the number of vertices, \[F\] is the number of faces and \[E\] is the number of edges then \[V - E + F = 2\] . Then it is evident that a cube or cuboid is a three-dimensional figure that has \[12\] edges, \[8\] vertices, and \[6\] faces and hence we get the result.

Complete step by step answer:
First of all, let’s recall the definitions of faces, edges, and vertices.
Faces: The flat surfaces that are made up of the outside of a shape are called the faces.
Edges: Edges are the lines in between the faces.
Vertices: Vertices are the corner points where two or more edges of the solid figure meet.
Now we will check whether the given dimensions form a valid three-dimensional figure or not.
By Euler’s Polyhedral Formula
We know that in a convex polyhedral, if \[V\] is the number of vertices, \[F\] is the number of faces and \[E\] is the number of edges then
\[V - E + F = 2\]
Here, \[V = 8\]
\[E = 12\]
\[F = 6\]
On putting the values, we get
\[8 - 12 + 6 = 2\]
\[ \Rightarrow 2 = 2\]
Hence, it is a valid three-dimensional figure.
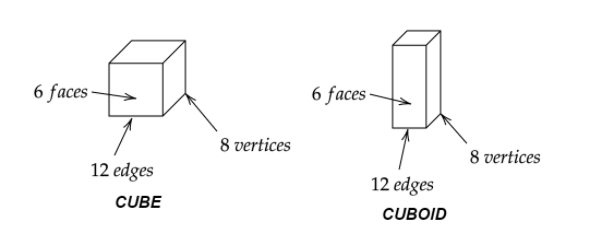
Now it is evident that the figure is cube or cuboid because a cube or cuboid is a three-dimensional figure that has \[12\] edges, \[8\] vertices, and \[6\] faces.

Note:
The difference between a cube and cuboid is that a cube has all edges equal which makes every face a square while a cuboid has two square faces and four rectangular faces. In a cube all edges and faces are equal while in cuboid opposite faces and edges are equal.
Dimensions of some more examples of three-dimensional shapes:
A Prism: \[9\] edges, \[6\] vertices, and \[5\] faces.
A Pyramid: \[8\] edges, \[5\] vertices, and \[5\] faces.
A Cylinder: \[2\] edges, \[0\] vertex, and \[3\] faces ( \[2\] flat and \[1\] curved)
A Cone: \[1\] edge, \[1\] vertex, and \[2\] faces ( \[1\] flat and \[1\] curved)
A Sphere: \[0\] edge, \[0\] vertex, and \[1\] curved face.