
Write down a unit vector in XY-plane, making an angle of
positive direction of x-axis.
Answer
536.1k+ views
1 likes
Hint: If a unit vector is making an angle
Before proceeding with the question, we must know the formula that will be required to solve this question. In vectors, if a unit vector is making an angle
In the question, we have to write down the unit vector making an angle
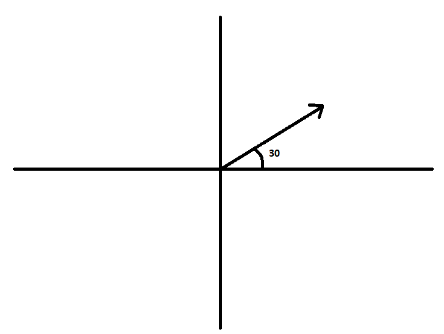
The x component of this vector will be
From trigonometry, we have
There is one more possible vector that can make an angle of
That vector is as shown below,
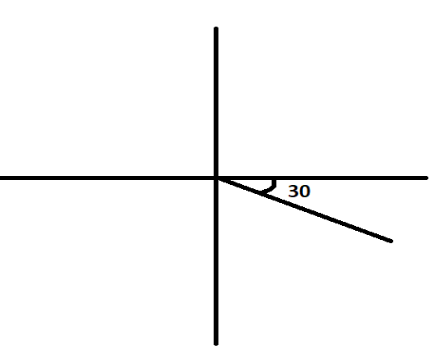
The x component of this vector will be
From trigonometry, we have
So, the two possible answers are
Note: In this question, we were given a unit vector which is making an angle of
Before proceeding with the question, we must know the formula that will be required to solve this question. In vectors, if a unit vector is making an angle
In the question, we have to write down the unit vector making an angle

The x component of this vector will be
From trigonometry, we have
There is one more possible vector that can make an angle of
That vector is as shown below,

The x component of this vector will be
From trigonometry, we have
So, the two possible answers are
Note: In this question, we were given a unit vector which is making an angle of
Latest Vedantu courses for you
Grade 11 Science PCM | CBSE | SCHOOL | English
CBSE (2025-26)
School Full course for CBSE students
₹41,848 per year
Recently Updated Pages
Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Class 12 Question and Answer - Your Ultimate Solutions Guide

Master Class 11 Economics: Engaging Questions & Answers for Success

Trending doubts
Draw a labelled sketch of the human eye class 12 physics CBSE

a Tabulate the differences in the characteristics of class 12 chemistry CBSE

Which one of the following is a true fish A Jellyfish class 12 biology CBSE

Why is the cell called the structural and functional class 12 biology CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Write the difference between solid liquid and gas class 12 chemistry CBSE




