Question

Write Faraday’s laws of electromagnetic induction and obtain an expression of induced e.m.f.

Answer 1

Hint: Faraday’s laws of electromagnetism are used extensively as the operating principles of transformers, inductors, and different types of electrical motors. The induced electromotive force (emf) in any closed circuit will be the same as the rate of change of the magnetic flux through the circuit.
Formula used: \[{{F}_{B}}=Bqv\], where B is the magnetic field, q is the charge and v is the velocity.
\[qE={{F}_{E}}=\dfrac{V}{l}\], where V is the potential difference and l is the length of the conductor.
\[\Phi =BA\], where B is the magnetic flux density and A is the area.

Complete step by step answer:
 Faraday’s first law states that, when a conductor is placed in a magnetic field, the relative motion between the conductor and magnetic field produces an induced emf.
For the experimental proof, we can move either the magnet or the conductor.
Faraday’s second law states that the magnitude of the induced emf is directly proportional to the rate change of magnetic flux.
If a conductor of length l moves with a speed v through a magnetic field. The electrons of the conductor will experience a force due to their motion in the magnetic field. Remember that electrons will flow in the opposite direction of the current.

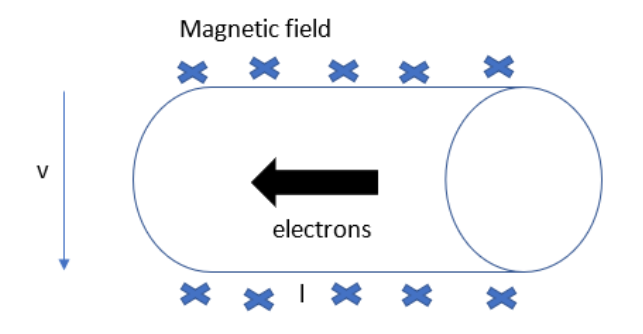
So the movement of charges will make a potential difference between the two ends of the conductor. Even if the charges want to come back to their initial position, the magnetic field and the motion of the conductor will not allow this.
If an external circuit is connected to this conductor, then the charges will flow through the circuit to achieve lower potential.
According to Flemming’s left-hand rule, the direction of the force will be in the upward direction. For the conservation of energy, the flowing current will make its force on the conductor.

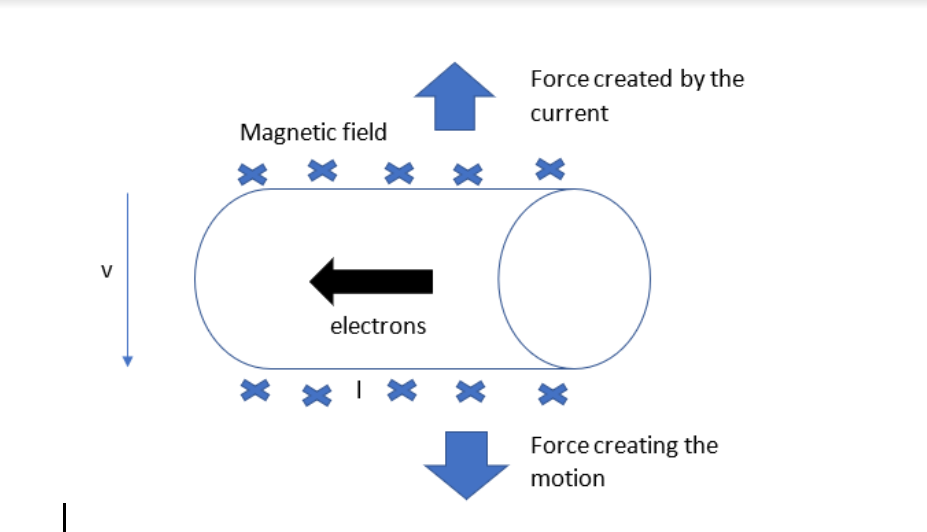
The charge separation will make an electric field force \[({{F}_{E}})\] in the direction of the current. The balancing force will be the magnetic field force \[({{F}_{B}})\].
\[{{F}_{B}}={{F}_{E}}\]
Here the magnetic force can be written as,
\[{{F}_{B}}=Bqv\], where B is the magnetic field, q is the charge and v is the velocity.
\[qE={{F}_{E}}=\dfrac{V}{l}\], where V is the potential difference and l is the length of the conductor.
These two forces can be equated.
\[\dfrac{Vq}{l}=Bqv\]
From this, we can find out the potential difference.
\[V=Blv\]
This potential difference is known as induced emf.
The magnetic flux density is the number of magnetic field lines per unit area. So the total flux can be written as,
\[\Phi =BA\], where B is the magnetic flux density and A is the area.
In the induced emf equation you can see \[V=Blv\]
Here \[lv\] also represents the area through which the conductor moves per second.
So, we can substitute \[lv\] as the area per unit time.
\[V=\dfrac{BA}{t}\]
According to Faraday’s law, the change in flux will induce emf. Thus we can write as,
\[V=\dfrac{BA}{t}=\dfrac{d\Phi }{dt}\]
Note: The current flow is always opposite to the direction of the electrons flow. If there is no opposing force to the direction of motion of a conductor, then the initial push to the conductor in the magnetic field will create current forever. This is contradicting the law of conservation of energy.