Question

Write the condition of collinearity of three points \[A\left( {{x}_{1}},{{y}_{1}} \right),B\left( {{x}_{2}},{{y}_{2}} \right),C\left( {{x}_{3}},{{y}_{3}} \right).\]

Answer 1

Hint: First understand the definition of collinear points and their condition geometrically. Now, to write the condition of collinearity for the given points in the coordinate form, assume that these three points are forming a triangle and apply the formula for the area of the triangle given as \[\text{Area}=\dfrac{1}{2}\left[ {{x}_{1}}\left( {{y}_{2}}-{{y}_{3}} \right)+{{x}_{2}}\left( {{y}_{3}}-{{y}_{1}} \right)+{{x}_{3}}\left( {{y}_{1}}-{{y}_{2}} \right) \right].\] Equate this area relation with 0 to get the answer.

Complete step-by-step solution:
Here, we are provided with three points \[A\left( {{x}_{1}},{{y}_{1}} \right),B\left( {{x}_{2}},{{y}_{2}} \right),C\left( {{x}_{3}},{{y}_{3}} \right).\] We have been asked to find the condition of the collinearity for these points. But first, let us see the meaning of collinear points. In geometry, the collinear points are defined as a set of points that lie on a single line. This property of a set of points lying on a single line is called collinearity of the set of points. Now, for the term collinear points to be defined, we must have three points because two points are always collinear and for a single point, the term collinear is undefined. Let us see some examples.
(1)

Here we can see that we are able to draw a single straight line through the given three points P, Q, and R. So, they are collinear in nature.
(2)

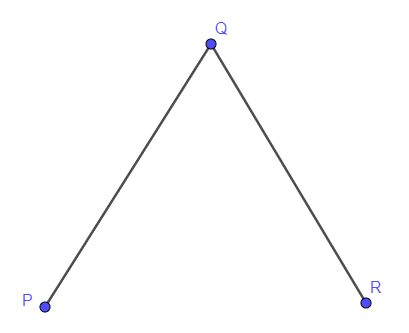
Here, in this case, we cannot draw a straight line through P, Q, and R, so they are non – collinear.
Now, let us come to the question. We have to assume that the given points A, B, and C are collinear because only then we can find the condition for non – collinearity. So, we have,

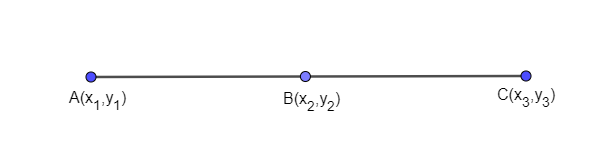
Since, we know that a triangle can be formed only when three points are non – collinear. Now, we can assume the above straight line formed by points A, B, and C as a triangle whose height is 0. So, we have,
\[\text{Area}=\dfrac{1}{2}\times base\times height\]
\[\Rightarrow \text{Area}=\dfrac{1}{2}\times base\times 0\]
\[\Rightarrow \text{Area}=0\]
Therefore, the condition for collinearity of three points is that its area should be 0.
Now, we have to find the collinearity condition in terms of the coordinate geometry. So, we know that the area relation of a triangle for points \[A\left( {{x}_{1}},{{y}_{1}} \right),B\left( {{x}_{2}},{{y}_{2}} \right),C\left( {{x}_{3}},{{y}_{3}} \right)\] is given as
\[\text{Area}=\dfrac{1}{2}\left[ {{x}_{1}}\left( {{y}_{2}}-{{y}_{3}} \right)+{{x}_{2}}\left( {{y}_{3}}-{{y}_{1}} \right)+{{x}_{3}}\left( {{y}_{1}}-{{y}_{2}} \right) \right]\]
So substituting area = 0, we get,
\[\Rightarrow \dfrac{1}{2}\left[ {{x}_{1}}\left( {{y}_{2}}-{{y}_{3}} \right)+{{x}_{2}}\left( {{y}_{3}}-{{y}_{1}} \right)+{{x}_{3}}\left( {{y}_{1}}-{{y}_{2}} \right) \right]=0\]
\[\Rightarrow \left[ {{x}_{1}}\left( {{y}_{2}}-{{y}_{3}} \right)+{{x}_{2}}\left( {{y}_{3}}-{{y}_{1}} \right)+{{x}_{3}}\left( {{y}_{1}}-{{y}_{2}} \right) \right]=0\]
Hence, the above obtained relation is our answer.

Note: One may note that without understanding the definition and properties of collinear points we cannot solve the above question. You must remember the formula for the area of the triangle geometrically, in terms of base and height, and in coordinate geometry also. Remember that if we would have been provided with 4 points then we would have applied the formula of area of a quadrilateral and substituted it equal to 0 to get the answer.