Question

Write the definition of electric potential. Calculate the electric potential due to a point charge Q at a distance r from it. Draw a graph between electric potential V and the distance r for a point charge Q.

Answer 1

Hint:Work done is the measure of electric potential($V$) in our case.
Work done by a unit charge to move from infinity to the specific distance r due to a point charge Q at a distance r is $V = - \mathop \smallint \nolimits_ \propto ^r Edx$.

Complete step by step answer:
Definition:The amount of work done due to the movement of a unit charge from an arbitrary point to a particular point because of the electric field generated by a point charge in that specific space is called electric potential.
Let us consider a point charge Q is there in space resulting in an electric field around it.
So the work done to bring a unit charge from an arbitrary point to the specific point( distance r from the charge Q ) can be calculated.
$V = - \mathop \smallint \nolimits_ \propto ^r Edx$ (where E is the electric field, and $dx$ is displacement negative sign is because the work is done against the electric field E)
$V = - \mathop \smallint \nolimits_ \propto ^r \dfrac{Q}{{4\pi {\varepsilon _0}{x^2}}}dx$ (Since electric field due to a point charge Q at a distance x is $E = \dfrac{Q}{{4\pi {\varepsilon _0}{x^2}}}$)
$V = - \dfrac{Q}{{4\pi {\varepsilon _0}}}\mathop \smallint \nolimits_ \propto ^r \dfrac{1}{{{x^2}}}dx$
$V = - \dfrac{Q}{{4\pi {\varepsilon _0}}}\left[ {\dfrac{1}{x}} \right]_ \propto ^r$
$V = \dfrac{Q}{{4\pi {\varepsilon _0}}}\left[ {\dfrac{1}{r} - \dfrac{1}{ \propto }} \right]$ (say $\dfrac{1}{ \propto } = 0$)
$V = \dfrac{Q}{{4\pi {\varepsilon _0}r}}$
Electric potential due to a point charge Q at a distance r from it is $V = \dfrac{Q}{{4\pi {\varepsilon _0}r}}$
Now the plot between the electrical potential V and the distance r for a point charge Q is shown below

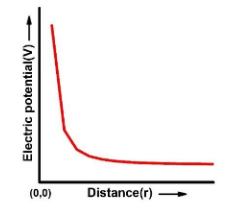
Note:Electrical potential is inversionally proportional to the squared distance from the charge and the SI unit of electric potential is volt.