Question

Write the formula of volume of cone.

Answer 1

Hint:
We will draw a figure of the cone. Then we will study the figure and describe the elements that make the cone. After that, we will give the formula for the volume of the cone. We will look at the relation of the volume of a cone with the volume of a cylinder that has the same radius and height. We will give an example of the application of the formula for the volume of a cone.

Complete step by step answer:
The following is the diagram of a cone,

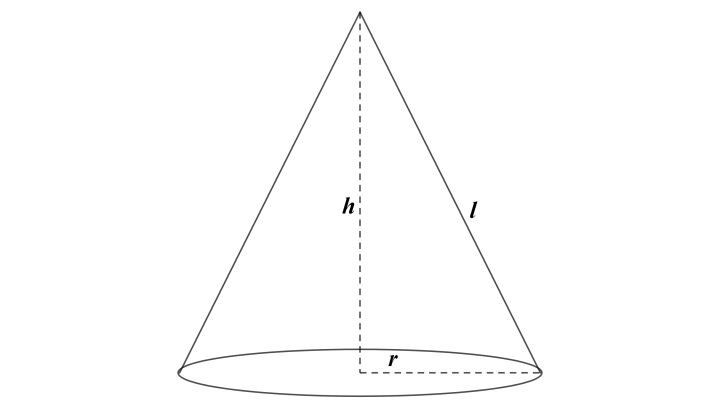
We have a cone with radius $ r $ , height $ h $ and slant height $ l $ . We can see that the base of the cone is circular. The area of the circular base is $ \pi {{r}^{2}} $ . The formula of the volume of cone is given as
 $ \text{volume of cone}=\dfrac{1}{3}\pi {{r}^{2}}h $
We know that the volume of the cylinder with radius $ r $ and height $ h $ is given as
 $ \text{volume of cylinder}=\pi {{r}^{2}}h $ .
So, we get the following relation between the volume of a cone and the volume of a cylinder,
 $ \text{volume of cone}=\dfrac{1}{3}\times \text{volume of cylinder} $
We need the formula for the volume of the cylinder since it has useful applications. An example of its application is to find the volume of liquid in a conical flask.
Note:
 We can derive the formula for the volume of the cone by using integration. For this, we will come up with a function in the Cartesian plane and then rotate this function about one axis. We will get a solid of revolution, a three-dimensional object, which will be the cone. We write the slant height in terms of the radius and height of the cone. Then we integrate along the height of the cone to obtain the volume of the cone.