
Write the relation between focal length and radius of curvature of a spherical mirror.
Answer
434.8k+ views
9 likes
Hint: Before stating the relation, derive the relation between radius of curvature and the focal length of a mirror. This will help you understand better. Use the fact that when a parallel ray of light falls on a concave mirror, it passes through the focus of the mirror after reflection.
Complete step by step answer:
The relation between focal length (f) and radius of curvature (R) of a spherical mirror is that the focal length is equal to half of the radius of curvature i.e.
Let us derive this relation.
Consider a concave mirror such that its radius of curvature is very much larger than the diameter of its aperture.
We can take help from the figure given.
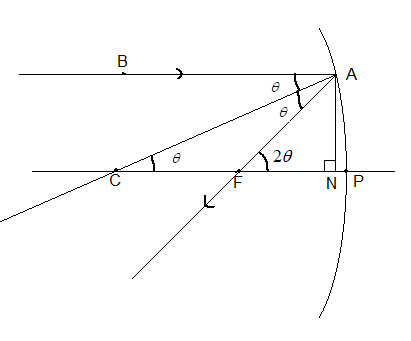
Suppose a parallel ray of light is incident on the mirror as shown in the figure. Let this incident ray make an angle
We know that rays of light parallel to the principal axis passing through the focus (F) of a concave mirror, after reflection.
According to the law of reflections, the angle of incidence and angle of reflection are equal. Therefore,
Since BA and PC are parallel,
Therefore, from exterior angle theorem
Now drop a normal CP from point A. Let the foot of this normal be N.
Here,
From equation (i) and equation (ii) we get,
Since the radius of curvature is very much larger than the diameter of its aperture, NP is very small compared to CN and CP and
Therefore,
For small angles
Therefore, equation (iii) can be written as
And CP=R and FP=f.
Hence,
Note: Note that this relation between the radius of curvature (R) of a concave mirror and the focal length (f) of the mirror, which is
Complete step by step answer:
The relation between focal length (f) and radius of curvature (R) of a spherical mirror is that the focal length is equal to half of the radius of curvature i.e.
Let us derive this relation.
Consider a concave mirror such that its radius of curvature is very much larger than the diameter of its aperture.
We can take help from the figure given.

Suppose a parallel ray of light is incident on the mirror as shown in the figure. Let this incident ray make an angle
We know that rays of light parallel to the principal axis passing through the focus (F) of a concave mirror, after reflection.
According to the law of reflections, the angle of incidence and angle of reflection are equal. Therefore,
Since BA and PC are parallel,
Therefore, from exterior angle theorem
Now drop a normal CP from point A. Let the foot of this normal be N.
Here,
From equation (i) and equation (ii) we get,
Since the radius of curvature is very much larger than the diameter of its aperture, NP is very small compared to CN and CP and
Therefore,
For small angles
Therefore, equation (iii) can be written as
And CP=R and FP=f.
Hence,
Note: Note that this relation between the radius of curvature (R) of a concave mirror and the focal length (f) of the mirror, which is
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Give 10 examples of unisexual and bisexual flowers

Draw a labelled sketch of the human eye class 12 physics CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE

What are the major means of transport Explain each class 12 social science CBSE

Why is the cell called the structural and functional class 12 biology CBSE




