
Write the value of
Answer
503.1k+ views
Hint: The above question is related to inverse trigonometric function and for solving the problem, you just have to put the values of
Complete step-by-step answer:
Before starting with the solution to the above question, we will first talk about the required details of different inverse trigonometric ratios. So, we must remember that inverse trigonometric ratios are completely different from trigonometric ratios and have many constraints related to their range and domain. So, to understand these constraints and the behaviour of inverse trigonometric functions, let us look at some of the important graphs. First, let us see the graph of
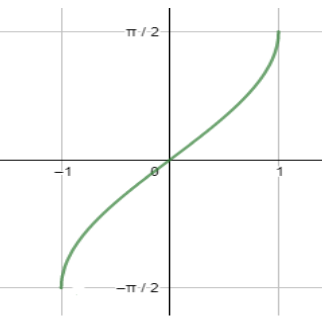
Now let us draw the graph of
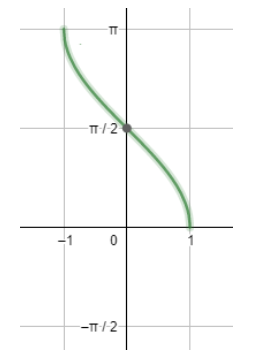
Also, we will draw the graph of
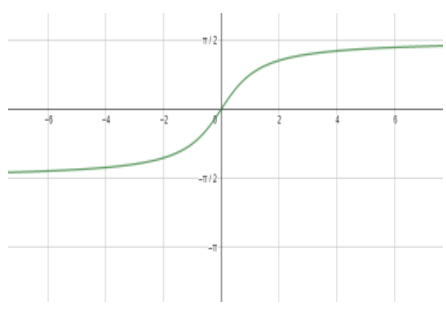
So, looking at the above graphs, we can draw the conclusion that
Now moving to the solution to the above question, we will start with the simplification of the expression given in the question.
We know that
We also know that
Therefore, the value of
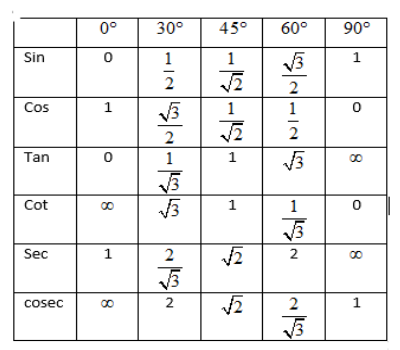
Note: Be careful about the range and domain of different trigonometric inverse functions as they are very confusing and may lead to errors. Don’t miss the final negative sign while reporting the answer. It is also important that you learn the trigonometric table which is as follow:
Complete step-by-step answer:
Before starting with the solution to the above question, we will first talk about the required details of different inverse trigonometric ratios. So, we must remember that inverse trigonometric ratios are completely different from trigonometric ratios and have many constraints related to their range and domain. So, to understand these constraints and the behaviour of inverse trigonometric functions, let us look at some of the important graphs. First, let us see the graph of

Now let us draw the graph of

Also, we will draw the graph of

So, looking at the above graphs, we can draw the conclusion that
Now moving to the solution to the above question, we will start with the simplification of the expression given in the question.
We know that
We also know that
Therefore, the value of
Note: Be careful about the range and domain of different trigonometric inverse functions as they are very confusing and may lead to errors. Don’t miss the final negative sign while reporting the answer. It is also important that you learn the trigonometric table which is as follow:

Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Give 10 examples of unisexual and bisexual flowers

Draw a labelled sketch of the human eye class 12 physics CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE

What are the major means of transport Explain each class 12 social science CBSE

Why is the cell called the structural and functional class 12 biology CBSE




