Question

Write the working of cyclotron in brief. Draw a schematic sketch of the cyclotron showing the path of accelerated charged particles (ions) in the Dees.
Derive the following parameters of cyclotron:
(a) Cyclotron frequency and
(b) Kinetic energy of ions of cyclotron.

Answer 1

Hint:Cyclotron is a famous particle accelerator that is used to study the behaviour of high velocity charged particles. A charged particle is introduced inside the vacuum chamber of a cyclotron. It is accelerated using an electric field, and the path is controlled using the magnetic field. When the charged particle leaves the cyclotron it can have a large value of Kinetic energy.


Complete step by step solution:
Let us first look at the following simplistic diagram of the cyclotron.

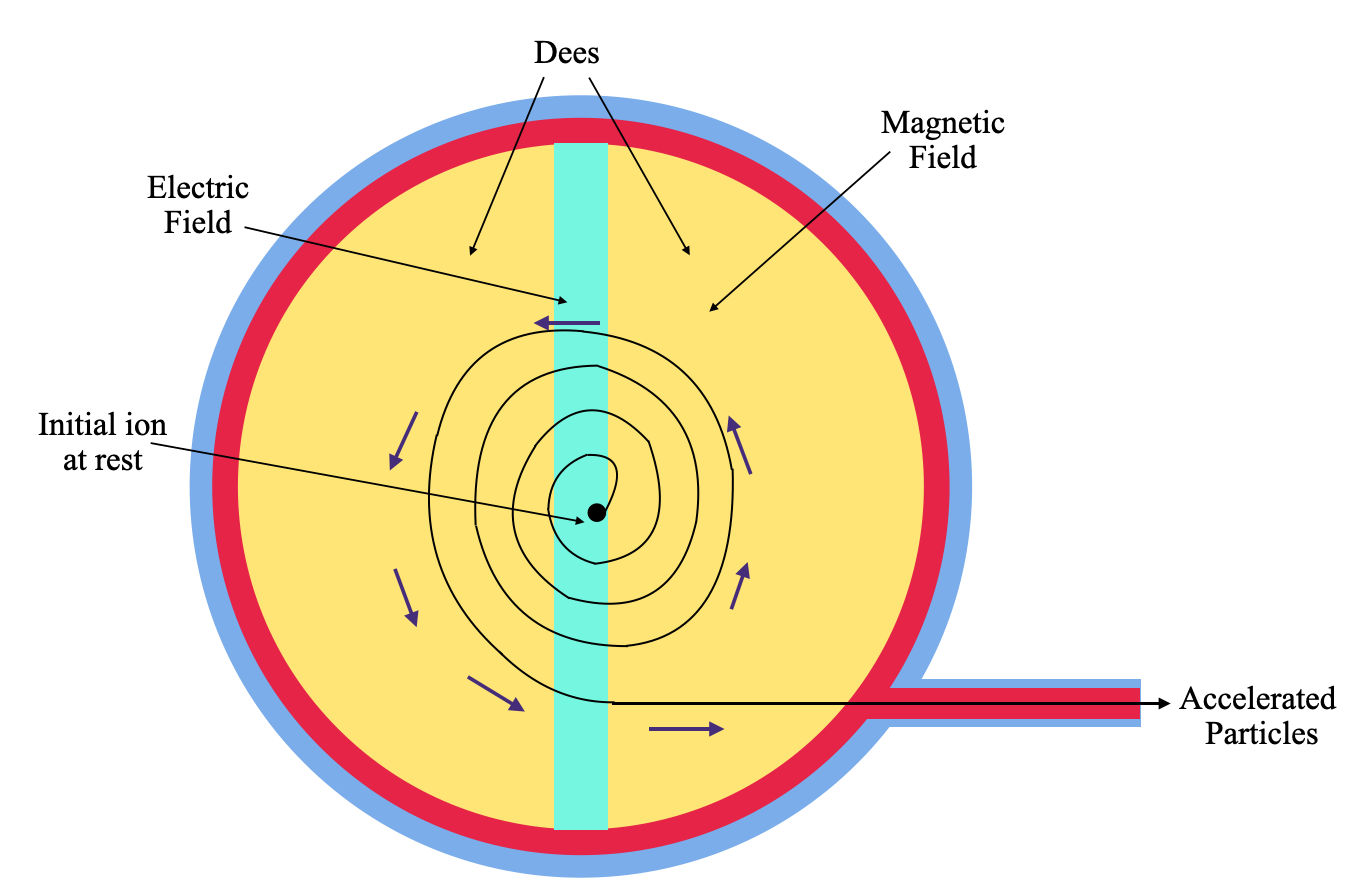
As you can see the cyclotron is a two separate D-shaped vacuum spaces separated by a high voltage electric field. The working principle is as follows-

1. At first, a charged particle is introduced inside the electric field region of the cyclotron. This electric field accelerates the charged particle and pushes it into the magnetic field region.



2. In the magnetic field region, it completes a half-circle without reducing its speed.

3. Magnetic field exerts a force perpendicular to the motion of the charged particle which helps to maintain a constant radius when it is inside the magnetic field region.

4. When the charged particle enters the electric field, it is accelerated further.

5. The increased velocity will force the particle to move in a bigger circle when it enters the magnetic field in the other Dee.

6. After another half rotation, the electric field in the region must be changed so that the charged particle can be accelerated again. Hence, we use an alternating electric field where the frequency of the voltage is set so that the particle makes one revolution during a single cycle of the voltage.

Cyclotron Frequency:

Let’s assume that the charge and mass of the particle is $q$ and $m$.

The magnetic field inside the medium is B.

Let’s assume the particle is moving at$v$ with a radius $r$.

Hence, the centripetal force is given by.
${\displaystyle \frac{m{v}^2}{r}}$

Magnetic force on the moving particle is given by,
$qvB$

As these two forces must be same, we can write,
$qvB={\displaystyle \frac{m{v}^2}{r}}$
$\Rightarrow v={\displaystyle \frac{qBr}{m}}$

So, the time required to complete one revolution is,
$T={\displaystyle \frac{2\pi r}{v}}={\displaystyle \frac{2\pi r}{\left({\displaystyle \frac{qBr}{m}}\right)}}={\displaystyle \frac{2\pi m}{qB}}$

Hence, the frequency of the particle is,
$f={\displaystyle \frac{1}{T}}={\displaystyle \frac{qB}{2\pi m}}$

As cyclotron frequency must be same as the frequency of the particle, we can write,
$f={\displaystyle \frac{qB}{2\pi m}}$

As we have already found the velocity of the particle, we can write the energy as,
${\displaystyle \frac{1}{2}}m{v}^2={\displaystyle \frac{1}{2}}m{\left({\displaystyle \frac{qBr}{m}}\right)}^2={\displaystyle \frac{q^2{B}^2{r}^2}{2m}}$



Note:This was one of the most famous particle accelerator machines in the domain of nuclear physics. These instruments have been replaced by other state-of-the-art machines which are more efficient and convenient. However, there are a lot of places where these machines are used for small scale experimental purposes.