Question

You are given one hundred $ 1\Omega $ resistors. What is the smallest and largest resistance you can make in a circuit using these?

Answer 1

Hint: The smallest resistance is obtained when all the resistors are connected in parallel combination. The largest resistance can be obtained when the resistors are connected in series combination. The series combination of resistance is the algebraic sum of the values while the parallel resistance is the algebraic sum of the reciprocal of the values.
The formula for equivalent resistance $ \left( {{R_p}} \right) $ for parallel combination is given by the equation:
 $ \dfrac{1}{{{R_p}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} + ..... + \dfrac{1}{{{R_n}}} $ $ - - - - (1) $
Where, $ n = $ number of resistors.
Here, the subscript “ $ p $ ” in “ $ {R_p} $ ” denotes "parallel".
The formula for equivalent resistance $ ({R_s}) $ for series combination is given by the equation:
 $ {R_s} = {R_1} + {R_2} + ..... + {R_n} $ $ - - - - (2) $
Where, $ n = $ number of resistors.
Here, the subscript “ $ s $ ” in “ $ {R_s} $ ” denotes "series".

Complete answer:
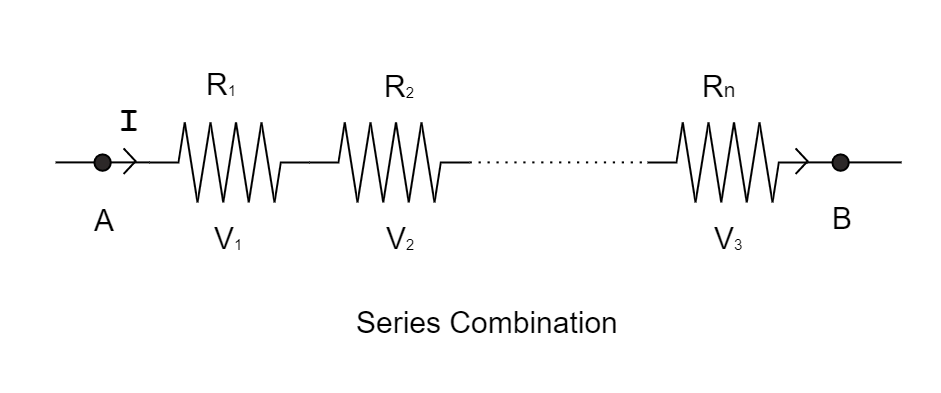
A number of resistances are said to be connected in series if they are joined end to end and the same current flows through each one of them but different voltage across each of the components.

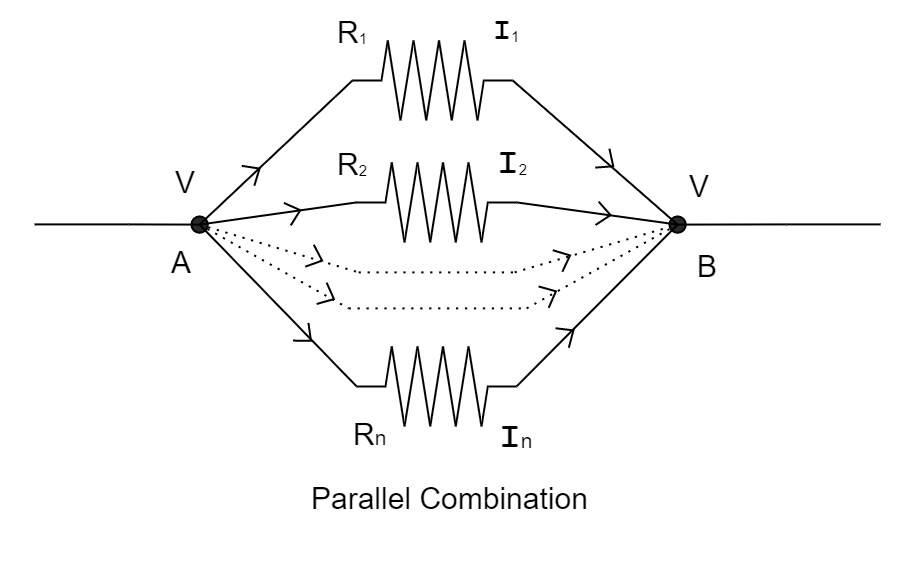
A number of resistances are said to be connected in parallel if they are joined between the same two ends with same voltage across each of the components but different current flow through each of them.

Given, The number of $ 1\Omega $ resistor $ = 100 $
Now, in order to obtain the smallest resistance using one hundred $ 1\Omega$ resistors , we connect the resistors in parallel. By the concept of resistances in parallel, the equivalent resistance is given by the reciprocal of the sum of the reciprocal of the resistors connected in parallel. Therefore, from equation $ (1) $ we have –
  $
  \dfrac{1}{{{R_p}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} + ..... + \dfrac{1}{{{R_n}}} \\
  \dfrac{1}{{{R_p}}} = \dfrac{1}{{{1_1}}} + \dfrac{1}{{{1_2}}} + ..... + \dfrac{1}{{{1_{100}}}} \\ [\because {R_1} = {R_2} = ..... = {R_{100}} = 1\Omega {\text{]}} \\
  \dfrac{1}{{{R_p}}} = {1_1} + {1_2} + ..... + {1_{100}} \\
  \dfrac{1}{{{R_p}}}{\text{ = 100}} \\
  $
By taking reciprocal on both sides, we get –
 $ {R_p} = \dfrac{1}{{100}} = 0.01\Omega $
Now, in order to obtain the largest resistance using one hundred $ 1\Omega $ resistors, we connect the resistors in series. By the concept of resistances in series, the equivalent resistance is given by the sum of the resistors connected in series. Therefore, from equation $ (2) $ we have –
 $
  {R_s} = {R_1} + {R_2} + ..... + {R_n} \\
  {R_s} = {1_1} + {1_2} + ..... + {1_{100}} \\
[\because {R_1} = {R_2} = ..... = {R_{100}} = 1\Omega ] \\
  {R_s} = 100\Omega \\
  $
Therefore, The required smallest resistance we can make with one hundred $ 1\Omega $ resistor $ = 0.01\Omega $
Also, The required smallest resistance we can make with one hundred $ 1\Omega $ resistor $ = 100\Omega $

Note:
The equivalent resistance will always be less than the value of the smallest resistance in parallel combination as the equivalent resistance is the sum of reciprocal of the individual resistances. The equivalent resistance series will always be greater than the individual resistances as it is the algebraic sum of individual resistance.